scipy.interpolate.

CubicSpline#

класс scipy.interpolate.CubicSpline(x, y, ось=0, bc_type='not-a-knot', экстраполяция=None)[источник]#

Кусочно-кубический интерполятор для подгонки значений (C2 гладкий).

Интерполировать данные кусочно-кубическим полиномом, который дважды непрерывно дифференцируем [1]. Результат представлен как PPoly экземпляр с точками останова, соответствующими предоставленным данным.

Параметры:

xarray_like, форма (n,)

1-D массив, содержащий значения независимой переменной. Значения должны быть вещественными, конечными и строго возрастающими.

yarray_like

Массив, содержащий значения зависимой переменной. Он может иметь произвольное количество измерений, но длина вдоль axis (см. ниже) должна соответствовать длине x. Значения должны быть конечными.

осьint, необязательный

Ось, вдоль которой y предполагается изменяющимся. Это означает, что для x[i] соответствующие значения — np.take(y, i, axis=axis). По умолчанию 0.

bc_typeстрока или 2-кортеж, опционально

Тип граничного условия. Два дополнительных уравнения, заданных граничными условиями, требуются для определения всех коэффициентов полиномов на каждом сегменте [2].

Если bc_type является строкой, то указанное условие будет применено на обоих концах сплайна. Доступные условия:

‘not-a-knot’ (по умолчанию): Первый и второй сегменты на конце кривой являются одним и тем же полиномом. Это хорошее значение по умолчанию, когда нет информации о граничных условиях.
‘periodic’: Предполагается, что интерполируемые функции периодичны с периодом x[-1] - x[0]. Первое и последнее значение y должны быть идентичными: y[0] == y[-1]. Это граничное условие приведет к y'[0] == y'[-1] и y''[0] == y''[-1].
‘clamped’: Первая производная на концах кривых равна нулю. Предполагая одномерный y, bc_type=((1, 0.0), (1, 0.0)) это то же условие.
‘natural’: Вторая производная на концах кривой равна нулю. Предполагая одномерный y, bc_type=((2, 0.0), (2, 0.0)) это то же условие.

Если bc_type является кортежем из двух элементов, первое и второе значения будут применены в начале и конце кривой соответственно. Значения кортежа могут быть одной из ранее упомянутых строк (кроме 'periodic') или кортежем (order, deriv_values) позволяя задавать произвольные производные на концах кривой:

порядок: порядок производной, 1 или 2.
deriv_value: array_like, содержащий значения производных, форма должна быть такой же, как y, исключая axis размерность. Например, если y является одномерным, тогда deriv_value должен быть скаляром. Если y является 3-D с формой (n0, n1, n2) и axis=2, тогда deriv_value должен быть двумерным и иметь форму (n0, n1).

экстраполяция{bool, 'periodic', None}, опционально

Если bool, определяет, следует ли экстраполировать на точки вне границ на основе первого и последнего интервалов или возвращать NaN. Если 'periodic', используется периодическая экстраполяция. Если None (по умолчанию), extrapolate установлен в 'periodic' для bc_type='periodic' и в True в противном случае.

Атрибуты:

xndarray, форма (n,): Точки останова. The same x который был передан конструктору.
cndarray, форма (4, n-1, …): Коэффициенты полиномов на каждом сегменте. Задние размерности соответствуют размерам y, исключая axis. Например, если y является одномерным, тогда c[k, i] является коэффициентом для (x-x[i])**(3-k) на отрезке между x[i] и x[i+1].
осьint: Ось интерполяции. Та же ось, которая была передана в конструктор.

Методы

`__call__`(x[, nu, extrapolate])	Вычислить кусочно-полиномиальную функцию или её производную.
`derivative`([nu])	Создать новый кусочно-полиномиальный объект, представляющий производную.
`antiderivative`([nu])	Создать новый кусочно-полиномиальный объект, представляющий первообразную.
`integrate`(a, b[, extrapolate])	Вычислить определённый интеграл по кусочно-полиномиальной функции.
`solve`([y, разрыв, экстраполяция])	Найти вещественные решения уравнения `pp(x) == y`.
`roots`([discontinuity, extrapolate])	Найти вещественные корни кусочно-полиномиальной функции.

Смотрите также

Akima1DInterpolator: Интерполятор Akima 1D.
PchipInterpolator: PCHIP 1-D монотонный кубический интерполятор.
PPoly: Кусочно-полиномиальная функция в терминах коэффициентов и точек разрыва.

Примечания

Параметры bc_type и extrapolate работают независимо, т.е. первый управляет только построением сплайна, а второй только вычислением.

Когда граничное условие 'not-a-knot' и n = 2, оно заменяется условием, что первая производная равна наклону линейного интерполянта. Когда оба граничных условия 'not-a-knot' и n = 3, решение ищется как парабола, проходящая через заданные точки.

Когда граничные условия 'not-a-knot' применяются к обоим концам, результирующий сплайн будет таким же, как возвращаемый splrep (с s=0) и InterpolatedUnivariateSpline, но эти два метода используют представление в базисе B-сплайнов.

Добавлено в версии 0.18.0.

Ссылки

[1]

Интерполяция кубическими сплайнами на Wikiversity.

[2]

Карл де Бур, «Практическое руководство по сплайнам», Springer-Verlag, 1978.

Примеры

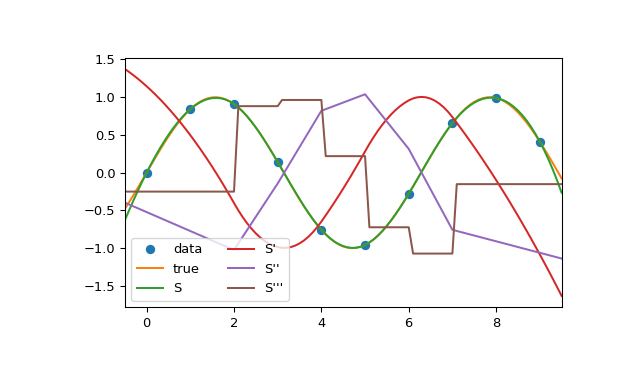
В этом примере кубический сплайн используется для интерполяции дискретизированного синусоидального сигнала. Вы можете видеть, что свойство непрерывности сплайна выполняется для первой и второй производных и нарушается только для третьей производной.

>>> import numpy as np
>>> from scipy.interpolate import CubicSpline
>>> import matplotlib.pyplot as plt
>>> x = np.arange(10)
>>> y = np.sin(x)
>>> cs = CubicSpline(x, y)
>>> xs = np.arange(-0.5, 9.6, 0.1)
>>> fig, ax = plt.subplots(figsize=(6.5, 4))
>>> ax.plot(x, y, 'o', label='data')
>>> ax.plot(xs, np.sin(xs), label='true')
>>> ax.plot(xs, cs(xs), label="S")
>>> ax.plot(xs, cs(xs, 1), label="S'")
>>> ax.plot(xs, cs(xs, 2), label="S''")
>>> ax.plot(xs, cs(xs, 3), label="S'''")
>>> ax.set_xlim(-0.5, 9.5)
>>> ax.legend(loc='lower left', ncol=2)
>>> plt.show()

../../_images/scipy-interpolate-CubicSpline-1_00_00.png

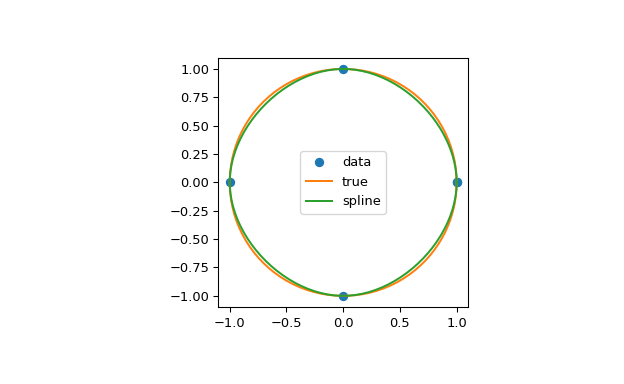
Во втором примере единичная окружность интерполируется сплайном. Используется периодическое граничное условие. Можно видеть, что значения первой производной, ds/dx=0, ds/dy=1 в периодической точке (1, 0) вычислены корректно. Заметим, что окружность не может быть точно представлена кубическим сплайном. Для повышения точности потребовалось бы больше точек разрыва.

>>> theta = 2 * np.pi * np.linspace(0, 1, 5)
>>> y = np.c_[np.cos(theta), np.sin(theta)]
>>> cs = CubicSpline(theta, y, bc_type='periodic')
>>> print("ds/dx={:.1f} ds/dy={:.1f}".format(cs(0, 1)[0], cs(0, 1)[1]))
ds/dx=0.0 ds/dy=1.0
>>> xs = 2 * np.pi * np.linspace(0, 1, 100)
>>> fig, ax = plt.subplots(figsize=(6.5, 4))
>>> ax.plot(y[:, 0], y[:, 1], 'o', label='data')
>>> ax.plot(np.cos(xs), np.sin(xs), label='true')
>>> ax.plot(cs(xs)[:, 0], cs(xs)[:, 1], label='spline')
>>> ax.axes.set_aspect('equal')
>>> ax.legend(loc='center')
>>> plt.show()

../../_images/scipy-interpolate-CubicSpline-1_01_00.png

Третий пример — интерполяция полинома y = x**3 на интервале 0 <= x <= 1. Кубический сплайн может точно представить эту функцию. Для этого необходимо указать значения и первые производные на концах интервала. Обратите внимание, что y' = 3 * x**2, и, следовательно, y'(0) = 0 и y'(1) = 3.

>>> cs = CubicSpline([0, 1], [0, 1], bc_type=((1, 0), (1, 3)))
>>> x = np.linspace(0, 1)
>>> np.allclose(x**3, cs(x))
True