scipy.interpolate.BSpline.

basis_element

метод класса BSpline.basis_element(t, экстраполяция=True)

Возвращает базисный элемент B-сплайна B(x | t[0], ..., t[k+1]).

Параметры:

tndarray, форма (k+2,)

внутренние узлы

экстраполяцияbool или 'periodic', опционально

следует ли экстраполировать за пределы базового интервала, t[0] .. t[k+1]или возвращать nan. Если ‘periodic’, используется периодическая экстраполяция. По умолчанию True.

Возвращает:

basis_elementcallable

Вызываемый объект, представляющий базисный элемент B-сплайна для вектора узлов t.

Примечания

Степень B-сплайна, k, выводится из длины t как len(t)-2. Вектор узлов строится путём добавления и предварения k+1 элементы во внутренние узлы t.

Примеры

Попробуйте в вашем браузере!

Построить кубический B-сплайн:

>>> import numpy as np
>>> from scipy.interpolate import BSpline
>>> b = BSpline.basis_element([0, 1, 2, 3, 4])
>>> k = b.k
>>> b.t[k:-k]
array([ 0.,  1.,  2.,  3.,  4.])
>>> k
3

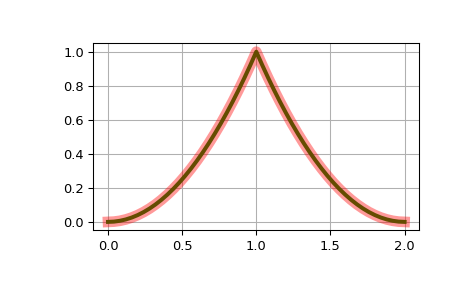
Постройте квадратичный B-сплайн на [0, 1, 1, 2], и сравнить с его явной формой:

>>> t = [0, 1, 1, 2]
>>> b = BSpline.basis_element(t)
>>> def f(x):
...     return np.where(x < 1, x*x, (2. - x)**2)

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> x = np.linspace(0, 2, 51)
>>> ax.plot(x, b(x), 'g', lw=3)
>>> ax.plot(x, f(x), 'r', lw=8, alpha=0.4)
>>> ax.grid(True)
>>> plt.show()

НазадОткрыть во вкладке