scipy.interpolate.

BSpline#

класс scipy.interpolate.BSpline(t, c, k, экстраполяция=True, ось=0)[источник]#

Одномерный сплайн в базисе B-сплайнов.

\[S(x) = \sum_{j=0}^{n-1} c_j B_{j, k; t}(x)\]

где $B_{j, k; t}$ являются B-сплайн базисными функциями степени k и узлы t.

Параметры:

tndarray, форма (n+k+1,): узлы
cndarray, форма (>=n, …): коэффициенты сплайна
kint: Степень B-сплайна
экстраполяцияbool или 'periodic', опционально: следует ли экстраполировать за пределы базового интервала, t[k] .. t[n], или для возврата nan. Если True, экстраполирует первый и последний полиномиальные участки b-сплайновых функций, активных на базовом интервале. Если ‘periodic’, используется периодическая экстраполяция. По умолчанию True.
осьint, необязательный: Ось интерполяции. По умолчанию равна нулю.

Атрибуты:

tndarray: вектор узлов
cndarray: коэффициенты сплайна
kint: степень сплайна
экстраполяцияbool: Если True, экстраполирует первый и последний полиномиальные сегменты b-сплайн функций, активных на базовом интервале.
осьint: Ось интерполяции.
tckкортеж: Эквивалентно (self.t, self.c, self.k) (только для чтения).

Методы

`__call__`(x[, nu, extrapolate])	Вычислить сплайн-функцию.
`basis_element`(t[, extrapolate])	Возвращает базисный элемент B-сплайна `B(x \| t[0], ..., t[k+1])`.
`derivative`([nu])	Вернуть B-сплайн, представляющий производную.
`antiderivative`([nu])	Возвращает B-сплайн, представляющий первообразную.
`integrate`(a, b[, extrapolate])	Вычислить определённый интеграл сплайна.
`insert_knot`(x[, m])	Вставить новый узел в x кратности m.
`construct_fast`(t, c, k[, extrapolate, axis])	Построить сплайн без проверок.
`design_matrix`(x, t, k[, extrapolate])	Возвращает матрицу плана в виде разреженного массива в формате CSR.
`from_power_basis`(pp[, bc_type])	Построить полином в базисе B-сплайна из кусочно-полиномиальной функции в степенном базисе.

Примечания

Базисные элементы B-сплайнов определяются через

\[ \begin{align}\begin{aligned}B_{i, 0}(x) = 1, \textrm{if $t_i \le x < t_{i+1}$, otherwise $0$,}\\B_{i, k}(x) = \frac{x - t_i}{t_{i+k} - t_i} B_{i, k-1}(x) + \frac{t_{i+k+1} - x}{t_{i+k+1} - t_{i+1}} B_{i+1, k-1}(x)\end{aligned}\end{align} \]

Детали реализации

По крайней мере k+1 коэффициенты требуются для сплайна степени k, так что n >= k+1. Дополнительные коэффициенты, c[j] с j > n, игнорируются.
B-сплайновые базисные элементы степени k образуют разбиение единицы на базовый интервал, t[k] <= x <= t[n].

Ссылки

[1]

Том Лише и Кнут Моркен, Методы сплайнов, http://www.uio.no/studier/emner/matnat/ifi/INF-MAT5340/v05/undervisningsmateriale/

[2]

Карл де Бур, Практическое руководство по сплайнам, Springer, 2001.

Примеры

Переводя рекурсивное определение B-сплайнов в код Python, получаем:

>>> def B(x, k, i, t):
...    if k == 0:
...       return 1.0 if t[i] <= x < t[i+1] else 0.0
...    if t[i+k] == t[i]:
...       c1 = 0.0
...    else:
...       c1 = (x - t[i])/(t[i+k] - t[i]) * B(x, k-1, i, t)
...    if t[i+k+1] == t[i+1]:
...       c2 = 0.0
...    else:
...       c2 = (t[i+k+1] - x)/(t[i+k+1] - t[i+1]) * B(x, k-1, i+1, t)
...    return c1 + c2

>>> def bspline(x, t, c, k):
...    n = len(t) - k - 1
...    assert (n >= k+1) and (len(c) >= n)
...    return sum(c[i] * B(x, k, i, t) for i in range(n))

Обратите внимание, что это неэффективный (хотя и простой) способ вычисления B-сплайнов — этот класс сплайнов делает то же самое, но гораздо более эффективным способом.

Здесь мы строим квадратичную сплайн-функцию на базовом интервале 2 <= x <= 4 и сравните с наивным способом вычисления сплайна:

>>> from scipy.interpolate import BSpline
>>> k = 2
>>> t = [0, 1, 2, 3, 4, 5, 6]
>>> c = [-1, 2, 0, -1]
>>> spl = BSpline(t, c, k)
>>> spl(2.5)
array(1.375)
>>> bspline(2.5, t, c, k)
1.375

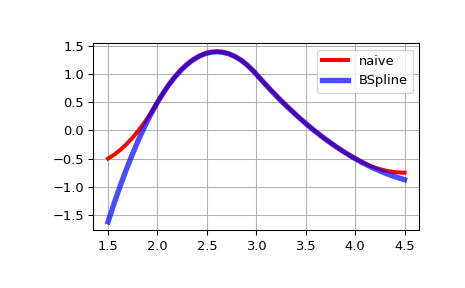
Обратите внимание, что за пределами базового интервала результаты отличаются. Это происходит потому, что BSpline экстраполирует первый и последний полиномиальные сегменты B-сплайновых функций, активных на базовом интервале.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> fig, ax = plt.subplots()
>>> xx = np.linspace(1.5, 4.5, 50)
>>> ax.plot(xx, [bspline(x, t, c ,k) for x in xx], 'r-', lw=3, label='naive')
>>> ax.plot(xx, spl(xx), 'b-', lw=4, alpha=0.7, label='BSpline')
>>> ax.grid(True)
>>> ax.legend(loc='best')
>>> plt.show()

../../_images/scipy-interpolate-BSpline-1.png