scipy.interpolate.LSQSphereBivariateSpline.

call#

LSQSphereBivariateSpline.__call__(theta, phi, dtheta=0, dphi=0, сетка=True)[источник]#

Вычисление сплайна или его производных в заданных позициях.

Параметры:

theta, phiarray_like

Входные координаты.

Если сетка равно False, вычислить сплайн в точках (theta[i], phi[i]), i=0, ..., len(x)-1. Стандартное вещание Numpy соблюдается.

Если сетка равно True: вычислить сплайн в точках сетки, определенных координатными массивами theta, phi. Массивы должны быть отсортированы в порядке возрастания. Порядок осей согласован с np.meshgrid(..., indexing="ij") и несовместимо с порядком по умолчанию np.meshgrid(..., indexing="xy").

dthetaint, необязательный

Порядок производной по тета

Добавлено в версии 0.14.0.

dphiint

Порядок производной по фи

Добавлено в версии 0.14.0.

сеткаbool

Оценивать ли результаты на сетке, порождённой входными массивами, или в точках, заданных входными массивами.

Добавлено в версии 0.14.0.

Примеры

Предположим, что мы хотим использовать сплайны для интерполяции двумерной функции на сфере. Значение функции известно на сетке долгот и широт.

>>> import numpy as np
>>> from scipy.interpolate import RectSphereBivariateSpline
>>> def f(theta, phi):
...     return np.sin(theta) * np.cos(phi)

Мы вычисляем функцию на сетке. Обратите внимание, что стандартная индексация="xy" в meshgrid приведет к неожиданному (транспонированному) результату после интерполяции.

>>> thetaarr = np.linspace(0, np.pi, 22)[1:-1]
>>> phiarr = np.linspace(0, 2 * np.pi, 21)[:-1]
>>> thetagrid, phigrid = np.meshgrid(thetaarr, phiarr, indexing="ij")
>>> zdata = f(thetagrid, phigrid)

Далее мы настраиваем интерполятор и используем его для вычисления функции на более мелкой сетке.

>>> rsbs = RectSphereBivariateSpline(thetaarr, phiarr, zdata)
>>> thetaarr_fine = np.linspace(0, np.pi, 200)
>>> phiarr_fine = np.linspace(0, 2 * np.pi, 200)
>>> zdata_fine = rsbs(thetaarr_fine, phiarr_fine)

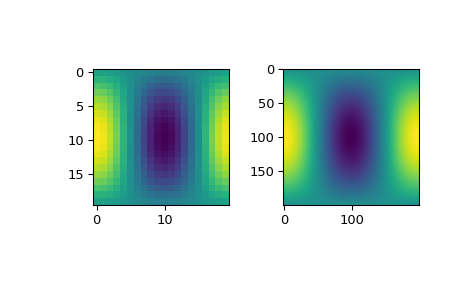
Наконец, мы строим график редко-дискретизированных входных данных вместе с часто-дискретизированными интерполированными данными, чтобы проверить их соответствие.

>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax1 = fig.add_subplot(1, 2, 1)
>>> ax2 = fig.add_subplot(1, 2, 2)
>>> ax1.imshow(zdata)
>>> ax2.imshow(zdata_fine)
>>> plt.show()

../../_images/scipy-interpolate-LSQSphereBivariateSpline-__call__-1.png

__call__#

call#