ev#
- LSQSphereBivariateSpline.ev(theta, phi, dtheta=0, dphi=0)[источник]#
Вычислить сплайн в точках
Возвращает интерполированное значение в
(theta[i], phi[i]), i=0,...,len(theta)-1.- Параметры:
- theta, phiarray_like
Входные координаты. Соблюдается стандартное вещание Numpy. Порядок осей согласуется с np.meshgrid(…, indexing="ij") и не согласуется с стандартным порядком np.meshgrid(…, indexing="xy").
- dthetaint, необязательный
Порядок производной по тета
Добавлено в версии 0.14.0.
- dphiint, необязательный
Порядок производной по фи
Добавлено в версии 0.14.0.
Примеры
Предположим, что мы хотим использовать сплайны для интерполяции двумерной функции на сфере. Значение функции известно на сетке долгот и широт.
>>> import numpy as np >>> from scipy.interpolate import RectSphereBivariateSpline >>> def f(theta, phi): ... return np.sin(theta) * np.cos(phi)
Мы вычисляем функцию на сетке. Обратите внимание, что стандартная индексация="xy" в meshgrid приведет к неожиданному (транспонированному) результату после интерполяции.
>>> thetaarr = np.linspace(0, np.pi, 22)[1:-1] >>> phiarr = np.linspace(0, 2 * np.pi, 21)[:-1] >>> thetagrid, phigrid = np.meshgrid(thetaarr, phiarr, indexing="ij") >>> zdata = f(thetagrid, phigrid)
Далее мы настраиваем интерполятор и используем его для вычисления функции в точках, не входящих в исходную сетку.
>>> rsbs = RectSphereBivariateSpline(thetaarr, phiarr, zdata) >>> thetainterp = np.linspace(thetaarr[0], thetaarr[-1], 200) >>> phiinterp = np.linspace(phiarr[0], phiarr[-1], 200) >>> zinterp = rsbs.ev(thetainterp, phiinterp)
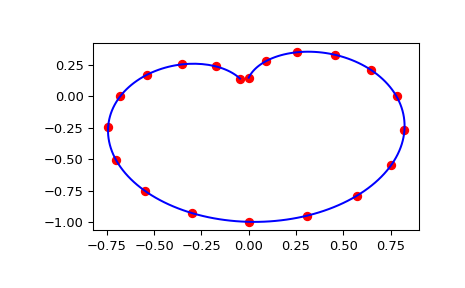
Наконец мы строим график исходных данных для диагонального среза через исходную сетку и сплайн-аппроксимацию вдоль того же среза.
>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax1 = fig.add_subplot(1, 1, 1) >>> ax1.plot(np.sin(thetaarr) * np.sin(phiarr), np.diag(zdata), "or") >>> ax1.plot(np.sin(thetainterp) * np.sin(phiinterp), zinterp, "-b") >>> plt.show()