RBFInterpolator#
- класс scipy.interpolate.RBFInterpolator(y, d, соседи=None, сглаживание=0.0, ядро='thin_plate_spline', эпсилон=None, степень=None)[источник]#
Интерполятор радиальных базисных функций в N ≥ 1 измерениях.
- Параметры:
- y(npoints, ndims) array_like
2-D массив координат точек данных.
- d(npoints, …) array_like
N-мерный массив значений данных в y. Длина d вдоль первой оси должно быть равно длине y. В отличие от некоторых интерполяторов, ось интерполяции не может быть изменена.
- соседиint, необязательный
Если указано, значение интерполянта в каждой точке оценки будет вычисляться с использованием только этого количества ближайших точек данных. По умолчанию используются все точки данных.
- сглаживаниеfloat или (npoints, ) array_like, опционально
Параметр сглаживания. Интерполянт идеально соответствует данным, когда этот параметр установлен в 0. При больших значениях интерполянт приближается к методу наименьших квадратов для полинома указанной степени. По умолчанию 0.
- ядроstr, optional
Тип RBF. Должен быть одним из
‘linear’ :
-r‘thin_plate_spline’ :
r**2 * log(r)'cubic' :
r**3'quintic' :
-r**5'multiquadric' :
-sqrt(1 + r**2)‘inverse_multiquadric’ :
1/sqrt(1 + r**2)'inverse_quadratic' :
1/(1 + r**2)'gaussian' :
exp(-r**2)
По умолчанию 'thin_plate_spline'.
- эпсилонfloat, опционально
Параметр формы, масштабирующий входные данные для RBF. Если ядро является ‘linear’, ‘thin_plate_spline’, ‘cubic’ или ‘quintic’, по умолчанию равно 1 и может быть проигнорировано, так как имеет тот же эффект, что и масштабирование параметра сглаживания. В противном случае это должно быть указано.
- степеньint, необязательный
Степень добавленного полинома. Для некоторых RBF интерполянт может быть плохо обусловлен, если степень полинома слишком мала. Эти RBF и их соответствующие минимальные степени:
‘multiquadric’ : 0
‘linear’ : 0
'thin_plate_spline' : 1
‘cubic’ : 1
'quintic' : 2
Значение по умолчанию — минимальная степень для ядро или 0, если нет минимальной степени. Установите значение -1 для отсутствия добавленного полинома.
Методы
__call__(x)Вычислить интерполянт в x.
Смотрите также
Примечания
RBF — это скалярная функция в N-мерном пространстве, значение которой в \(x\) может быть выражен через \(r=||x - c||\), где \(c\) является центром RBF.
Интерполянт RBF для вектора значений данных \(d\), которые из местоположений \(y\), является линейной комбинацией RBF, центрированных в \(y\) плюс полином указанной степени. RBF-интерполянт записывается как
\[f(x) = K(x, y) a + P(x) b,\]где \(K(x, y)\) это матрица RBF с центрами в \(y\) вычисленные в точках \(x\), и \(P(x)\) является матрицей мономов, которые охватывают полиномы указанной степени, вычисленные в \(x\). Коэффициенты \(a\) и \(b\) являются решением линейных уравнений
\[(K(y, y) + \lambda I) a + P(y) b = d\]и
\[P(y)^T a = 0,\]где \(\lambda\) является неотрицательным параметром сглаживания, который контролирует степень соответствия данным. Данные точно соответствуют модели, когда параметр сглаживания равен 0.
Вышеуказанная система однозначно разрешима, если выполнены следующие требования:
\(P(y)\) должен иметь полный ранг по столбцам. \(P(y)\) всегда имеет полный ранг столбцов, когда степень равно -1 или 0. Когда степень равен 1, \(P(y)\) имеет полный ранг по столбцам, если местоположения точек данных не все коллинеарны (N=2), компланарны (N=3) и т.д.
Если ядро если 'multiquadric', 'linear', 'thin_plate_spline', 'cubic' или 'quintic', то степень не должен быть ниже минимального значения, указанного выше.
Если сглаживание равно 0, тогда каждое местоположение точки данных должно быть уникальным.
При использовании RBF, не являющегося масштабно-инвариантным ('multiquadric', 'inverse_multiquadric', 'inverse_quadratic' или 'gaussian'), необходимо выбрать подходящий параметр формы (например, с помощью кросс-валидации). Меньшие значения параметра формы соответствуют более широким RBF. Задача может стать плохо обусловленной или сингулярной, если параметр формы слишком мал.
Память, необходимая для решения коэффициентов интерполяции RBF, растет квадратично с увеличением количества точек данных, что может стать непрактичным при интерполяции более чем около тысячи точек данных. Чтобы преодолеть ограничения памяти для больших задач интерполяции, соседи аргумент может быть указан для вычисления интерполянта RBF для каждой точки оценки, используя только ближайшие точки данных.
Добавлено в версии 1.7.0.
Ссылки
[1]Fasshauer, G., 2007. Meshfree Approximation Methods with Matlab. World Scientific Publishing Co.
[3]Wahba, G., 1990. Spline Models for Observational Data. SIAM.
Примеры
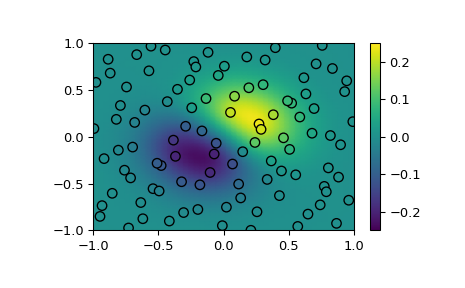
Демонстрация интерполяции разбросанных данных на сетку в 2-D.
>>> import numpy as np >>> import matplotlib.pyplot as plt >>> from scipy.interpolate import RBFInterpolator >>> from scipy.stats.qmc import Halton
>>> rng = np.random.default_rng() >>> xobs = 2*Halton(2, seed=rng).random(100) - 1 >>> yobs = np.sum(xobs, axis=1)*np.exp(-6*np.sum(xobs**2, axis=1))
>>> xgrid = np.mgrid[-1:1:50j, -1:1:50j] >>> xflat = xgrid.reshape(2, -1).T >>> yflat = RBFInterpolator(xobs, yobs)(xflat) >>> ygrid = yflat.reshape(50, 50)
>>> fig, ax = plt.subplots() >>> ax.pcolormesh(*xgrid, ygrid, vmin=-0.25, vmax=0.25, shading='gouraud') >>> p = ax.scatter(*xobs.T, c=yobs, s=50, ec='k', vmin=-0.25, vmax=0.25) >>> fig.colorbar(p) >>> plt.show()