scipy.interpolate.

CloughTocher2DInterpolator

класс scipy.interpolate.CloughTocher2DInterpolator(точки, values, fill_value=nan, tol=1e-06, maxiter=400, масштабировать=False)

Кусочно-кубический, C1-гладкий, минимизирующий кривизну интерполятор в N=2 измерениях.

Добавлено в версии 0.9.

Параметры:

точкиndarray чисел с плавающей точкой, форма (npoints, ndims); или Delaunay

2-D массив координат точек данных или предварительно вычисленная триангуляция Делоне.

valuesndarray из float или complex, форма (npoints, …)

N-мерный массив значений данных в точки. Длина values вдоль первой оси должно быть равно длине точки. В отличие от некоторых интерполяторов, ось интерполяции не может быть изменена.

fill_valuefloat, опционально

Значение, используемое для заполнения запрошенных точек вне выпуклой оболочки входных точек. Если не указано, то по умолчанию nan.

tolfloat, опционально

Абсолютная/относительная погрешность для оценки градиента.

maxiterint, необязательный

Максимальное количество итераций в оценке градиента.

масштабироватьbool, необязательно

Масштабировать точки до единичного куба перед выполнением интерполяции. Это полезно, если некоторые из входных измерений имеют несоизмеримые единицы и различаются на много порядков величины.

Методы

__call__(xi)

Вычислить интерполятор в заданных точках.

Смотрите также

griddata

Интерполяция неструктурированных D-D данных.

LinearNDInterpolator

Кусочно-линейный интерполятор в N > 1 измерениях.

NearestNDInterpolator

Интерполятор ближайшего соседа в N > 1 измерениях.

interpn

Интерполяция на регулярной или прямоугольной сетке.

RegularGridInterpolator

Интерполятор на регулярной или прямоугольной сетке в произвольных размерностях (interpn оборачивает этот класс).

Примечания

Интерполянт строится путем триангуляции входных данных с помощью Qhull [1], и построение кусочно-кубического интерполирующего полинома Безье на каждом треугольнике, используя схему Клафа-Токера [CT]. Интерполянт гарантированно непрерывно дифференцируем.

Градиенты интерполянта выбираются так, чтобы кривизна интерполирующей поверхности была приблизительно минимизирована. Необходимые для этого градиенты оцениваются с использованием глобального алгоритма, описанного в [Nielson83] и [Renka84].

Примечание

Для данных на регулярной сетке используйте interpn вместо этого.

Ссылки

[1]

http://www.qhull.org/

[CT]

См., например, P. Alfeld, ‘’A trivariate Clough-Tocher scheme for tetrahedral data’’. Computer Aided Geometric Design, 1, 169 (1984); G. Farin, ‘’Triangular Bernstein-Bezier patches’’. Computer Aided Geometric Design, 3, 83 (1986).

[Nielson83]

G. Nielson, 'Метод интерполяции разбросанных данных на основе сети минимальной нормы'. Math. Comp., 40, 253 (1983).

[Renka84]

R. J. Renka и A. K. Cline. «Метод C1 интерполяции на основе треугольников», Rocky Mountain J. Math., 14, 223 (1984).

Примеры

Попробуйте в вашем браузере!

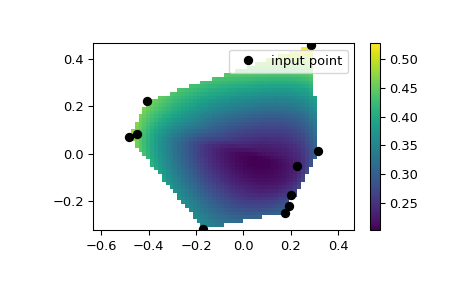
Мы можем интерполировать значения на двумерной плоскости:

>>> from scipy.interpolate import CloughTocher2DInterpolator
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> x = rng.random(10) - 0.5
>>> y = rng.random(10) - 0.5
>>> z = np.hypot(x, y)
>>> X = np.linspace(min(x), max(x))
>>> Y = np.linspace(min(y), max(y))
>>> X, Y = np.meshgrid(X, Y)  # 2D grid for interpolation
>>> interp = CloughTocher2DInterpolator(list(zip(x, y)), z)
>>> Z = interp(X, Y)
>>> plt.pcolormesh(X, Y, Z, shading='auto')
>>> plt.plot(x, y, "ok", label="input point")
>>> plt.legend(loc="upper right")
>>> plt.colorbar()
>>> plt.axis("equal")
>>> plt.show()

НазадОткрыть во вкладке