scipy.interpolate.

generate_knots#

scipy.interpolate.generate_knots(x, y, *, w=None, xb=None, xe=None, k=3, s=0, nest=None)[источник]#

Генерировать векторы узлов до тех пор, пока не будет удовлетворён критерий наименьших квадратов (LSQ).

Параметры:

x, yarray_like: Точки данных, определяющие кривую y = f(x).
warray_like, необязательный: Веса.
xbfloat, опционально: Граница интервала аппроксимации. Если None (по умолчанию), устанавливается в x[0].
xefloat, опционально: Граница интервала аппроксимации. Если None (по умолчанию), устанавливается в x[-1].
kint, необязательный: Степень сплайна. По умолчанию кубическая, k = 3.
sfloat, опционально: Коэффициент сглаживания. По умолчанию s = 0.
nestint, необязательный: Остановиться, когда размещено как минимум столько узлов.

Возвращает:

tndarray: Векторы узлов с увеличивающимся количеством узлов. Генератор конечен: он останавливается, когда критерий сглаживания удовлетворен, или когда количество узлов превышает максимальное значение: предоставленное пользователем nest или x.size + k + 1 — который является вектором узлов для интерполирующего сплайна.

Примечания

Подпрограмма генерирует последовательные векторы узлов увеличивающейся длины, начиная с 2*(k+1) to len(x) + k + 1, пытаясь сделать узлы более плотными в областях, где отклонение сплайна МНК от данных велико.

Когда максимальное количество узлов, len(x) + k + 1 достигается (это происходит, когда s мал и nest велико), генератор останавливается, и последний вывод — узлы для интерполяции с граничным условием not-a-knot.

Узлы расположены на сайтах данных, если только k чётное и количество узлов len(x) + k + 1. В этом случае последний вывод генератора имеет внутренние узлы в точках Гревиля, (x[1:] + x[:-1]) / 2.

Добавлено в версии 1.15.0.

Примеры

Сгенерировать некоторые зашумлённые данные и подогнать последовательность сплайнов МНК:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import make_lsq_spline, generate_knots
>>> rng = np.random.default_rng()
>>> x = np.linspace(-3, 3, 50)
>>> y = np.exp(-x**2) + 0.1 * rng.standard_normal(size=50)

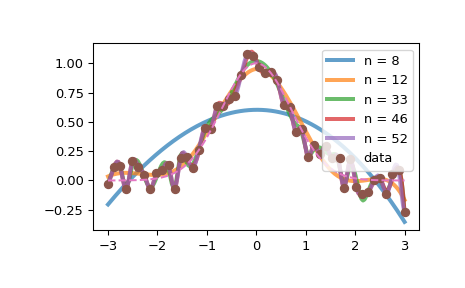
>>> knots = list(generate_knots(x, y, s=1e-10))
>>> for t in knots[::3]:
...     spl = make_lsq_spline(x, y, t)
...     xs = xs = np.linspace(-3, 3, 201)
...     plt.plot(xs, spl(xs), '-', label=f'n = {len(t)}', lw=3, alpha=0.7)
>>> plt.plot(x, y, 'o', label='data')
>>> plt.plot(xs, np.exp(-xs**2), '--')
>>> plt.legend()

Обратите внимание, что увеличение количества узлов делает результат всё более близким к данным.

Также обратите внимание, что шаг генератора может добавлять несколько узлов:

>>> [len(t) for t in knots]
[8, 9, 10, 12, 16, 24, 40, 48, 52, 54]

../../_images/scipy-interpolate-generate_knots-1.png