scipy.interpolate.

AAA

класс scipy.interpolate.AAA(x, y, *, rtol=None, max_terms=100, clean_up=True, clean_up_tol=1e-13)

Вещественная или комплексная рациональная аппроксимация AAA.

Как описано в [1], алгоритм AAA — это жадный алгоритм для аппроксимации рациональными функциями на множестве вещественных или комплексных точек. Рациональная аппроксимация представляется в барицентрической форме, из которой могут быть вычислены корни (нули), полюса и вычеты.

Параметры:

x1D array_like, форма (n,)

Одномерный массив, содержащий значения независимой переменной. Значения могут быть вещественными или комплексными, но должны быть конечными.

y1D array_like, форма (n,)

Значения функции f(x). Бесконечные и NaN значения values и соответствующие значения точки будет отброшен.

rtolfloat, опционально

Относительный допуск, по умолчанию eps**0.75. Если небольшое подмножество элементов в values намного больше остальных, то допуск по умолчанию может быть слишком свободным. Если допуск слишком жёсткий, то аппроксимация может содержать двойники Фруассара или алгоритм может полностью не сходиться.

max_termsint, необязательный

Максимальное количество членов в барицентрическом представлении, по умолчанию 100. Должно быть больше или равно единице.

clean_upbool, необязательно

Автоматическое удаление двойников Фруассара, по умолчанию True. См. примечания для подробностей.

clean_up_tolfloat, опционально

Полюса с вычетами меньше этого числа, умноженного на среднее геометрическое values раз минимальное расстояние до точки считаются ложными процедурой очистки, по умолчанию равно 1e-13. Подробнее см. в примечаниях.

Атрибуты:

support_pointsмассив

Опорные точки аппроксимации. Это подмножество предоставленных x в котором аппроксимация строго интерполирует y. См. примечания для более подробной информации.

support_valuesмассив

Значение аппроксимации в support_points.

весамассив

Веса барицентрической аппроксимации.

ошибкимассив

Ошибка \(|f(z) - r(z)|_\infty\) над точки в последовательных итерациях AAA.

Методы

__call__(z)	Вычислить рациональную аппроксимацию при заданных значениях.
clean_up([cleanup_tol])	Автоматическое удаление дублетов Фруассара.
poles()	Вычислить полюсы рациональной аппроксимации.
residues()	Вычислить вычеты полюсов аппроксимации.
roots()	Вычислить нули рациональной аппроксимации.

Предупреждает:

RuntimeWarning

Если rtol не достигается в max_terms итераций.

Смотрите также

FloaterHormannInterpolator

Барицентрическая рациональная интерполяция Флоатера-Хорманна.

pade

Аппроксимация Паде.

Примечания

На итерации \(m\) (в этот момент есть \(m\) члены как в числителе, так и в знаменателе аппроксимации), рациональная аппроксимация в алгоритме AAA принимает барицентрическую форму

\[r(z) = n(z)/d(z) = \frac{\sum_{j=1}^m\ w_j f_j / (z - z_j)}{\sum_{j=1}^m w_j / (z - z_j)},\]

где \(z_1,\dots,z_m\) являются вещественными или комплексными опорными точками, выбранными из x, \(f_1,\dots,f_m\) являются соответствующими действительными или комплексными значениями данных из y, и \(w_1,\dots,w_m\) являются вещественными или комплексными весами.

Каждая итерация алгоритма состоит из двух частей: жадного выбора следующей опорной точки и вычисления весов. Первая часть каждой итерации - выбрать следующую опорную точку для добавления \(z_{m+1}\) из оставшихся невыбранных x, так что нелинейный остаток \(|f(z_{m+1}) - n(z_{m+1})/d(z_{m+1})|\) максимизируется. Алгоритм завершается, когда этот максимум меньше rtol * np.linalg.norm(f, ord=np.inf). Это означает, что свойство интерполяции удовлетворяется только с точностью, за исключением опорных точек, где аппроксимация точно интерполирует предоставленные данные.

Во второй части каждой итерации веса \(w_j\) выбираются для решения задачи наименьших квадратов

\[\text{minimise}_{w_j}|fd - n| \quad \text{subject to} \quad \sum_{j=1}^{m+1} w_j = 1,\]

по невыбранным элементам x.

Одной из проблем при работе с рациональными приближениями является наличие двойников Фруассара, которые представляют собой либо полюса с исчезающе малыми вычетами, либо пары полюс-ноль, которые достаточно близки, чтобы почти сокращаться, см. [2]. Жадная природа алгоритма AAA означает, что двойники Фруассара редки. Однако, если rtol установлено слишком жестко, то аппроксимация застопорится и появится много двойников Фруассара. Двойники Фруассара обычно можно удалить, удалив опорные точки и затем повторно решив задачу наименьших квадратов. Опорная точка \(z_j\), который является ближайшей точкой опоры к полюсу \(a\) с остатком \(\alpha\), удаляется, если выполняется следующее условие

\[|\alpha| / |z_j - a| < \verb|clean_up_tol| \cdot \tilde{f},\]

где \(\tilde{f}\) является геометрическим средним support_values.

Ссылки

[1] (1,2,3)

Y. Nakatsukasa, O. Sete, и L. N. Trefethen, «Алгоритм AAA для рациональной аппроксимации», SIAM J. Sci. Comp. 40 (2018), A1494-A1522. DOI:10.1137/16M1106122

[2]

J. Gilewicz и M. Pindor, Pade approximants and noise: rational functions, J. Comp. Appl. Math. 105 (1999), pp. 285-297. DOI:10.1016/S0377-0427(02)00674-X

Примеры

Попробуйте в вашем браузере!

Здесь мы воспроизводим ряд численных примеров из [1] в качестве демонстрации функциональности, предлагаемой этим методом.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.interpolate import AAA
>>> import warnings

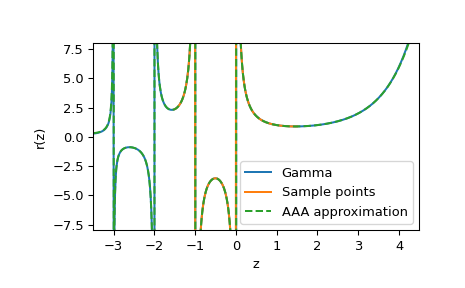
Для первого примера мы аппроксимируем гамма-функцию на [-3.5, 4.5] путем экстраполяции из 100 выборок в [-1.5, 1.5].

>>> from scipy.special import gamma
>>> sample_points = np.linspace(-1.5, 1.5, num=100)
>>> r = AAA(sample_points, gamma(sample_points))
>>> z = np.linspace(-3.5, 4.5, num=1000)
>>> fig, ax = plt.subplots()
>>> ax.plot(z, gamma(z), label="Gamma")
>>> ax.plot(sample_points, gamma(sample_points), label="Sample points")
>>> ax.plot(z, r(z).real, '--', label="AAA approximation")
>>> ax.set(xlabel="z", ylabel="r(z)", ylim=[-8, 8], xlim=[-3.5, 4.5])
>>> ax.legend()
>>> plt.show()

Мы также можем посмотреть полюса рациональной аппроксимации и их вычеты:

>>> order = np.argsort(r.poles())
>>> r.poles()[order]
array([-3.81591039e+00+0.j        , -3.00269049e+00+0.j        ,
       -1.99999988e+00+0.j        , -1.00000000e+00+0.j        ,
        5.85842812e-17+0.j        ,  4.77485458e+00-3.06919376j,
        4.77485458e+00+3.06919376j,  5.29095868e+00-0.97373072j,
        5.29095868e+00+0.97373072j])
>>> r.residues()[order]
array([ 0.03658074 +0.j        , -0.16915426 -0.j        ,
        0.49999915 +0.j        , -1.         +0.j        ,
        1.         +0.j        , -0.81132013 -2.30193429j,
       -0.81132013 +2.30193429j,  0.87326839+10.70148546j,
        0.87326839-10.70148546j])

Для второго примера мы вызываем AAA со спиралью из 1000 точек, которая делает 7,5 оборотов вокруг начала координат в комплексной плоскости.

>>> z = np.exp(np.linspace(-0.5, 0.5 + 15j*np.pi, 1000))
>>> r = AAA(z, np.tan(np.pi*z/2), rtol=1e-13)

Мы видим, что AAA занимает 12 шагов для сходимости со следующими ошибками:

>>> r.errors.size
12
>>> r.errors
array([2.49261500e+01, 4.28045609e+01, 1.71346935e+01, 8.65055336e-02,
       1.27106444e-02, 9.90889874e-04, 5.86910543e-05, 1.28735561e-06,
       3.57007424e-08, 6.37007837e-10, 1.67103357e-11, 1.17112299e-13])

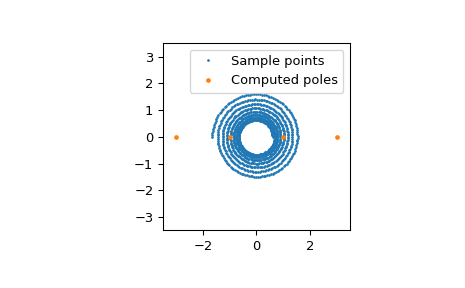
Мы также можем построить вычисленные полюсы:

>>> fig, ax = plt.subplots()
>>> ax.plot(z.real, z.imag, '.', markersize=2, label="Sample points")
>>> ax.plot(r.poles().real, r.poles().imag, '.', markersize=5,
...         label="Computed poles")
>>> ax.set(xlim=[-3.5, 3.5], ylim=[-3.5, 3.5], aspect="equal")
>>> ax.legend()
>>> plt.show()

Теперь мы демонстрируем удаление дублетов Фруассара с помощью clean_up метод на примере из [1]. Здесь мы аппроксимируем функцию \(f(z)=\log(2 + z^4)/(1 + 16z^4)\) путём выборки в 1000 корнях из единицы. Алгоритм запускается с rtol=0 и clean_up=False для намеренного создания дублетов Фруассара.

>>> z = np.exp(1j*2*np.pi*np.linspace(0,1, num=1000))
>>> def f(z):
...     return np.log(2 + z**4)/(1 - 16*z**4)
>>> with warnings.catch_warnings():  # filter convergence warning due to rtol=0
...     warnings.simplefilter('ignore', RuntimeWarning)
...     r = AAA(z, f(z), rtol=0, max_terms=50, clean_up=False)
>>> mask = np.abs(r.residues()) < 1e-13
>>> fig, axs = plt.subplots(ncols=2)
>>> axs[0].plot(r.poles().real[~mask], r.poles().imag[~mask], '.')
>>> axs[0].plot(r.poles().real[mask], r.poles().imag[mask], 'r.')

Теперь мы вызываем clean_up метод для удаления дублетов Фруассара.

>>> with warnings.catch_warnings():
...     warnings.simplefilter('ignore', RuntimeWarning)
...     r.clean_up()
4  # may vary
>>> mask = np.abs(r.residues()) < 1e-13
>>> axs[1].plot(r.poles().real[~mask], r.poles().imag[~mask], '.')
>>> axs[1].plot(r.poles().real[mask], r.poles().imag[mask], 'r.')
>>> plt.show()

Левое изображение показывает априорные полюса аппроксимации clean_up=False с полюсами, вычет которых меньше 10^-13 в абсолютном значении показаны красным. Правое изображение затем показывает полюса после clean_up метод был вызван.

НазадОткрыть во вкладке