scipy.linalg.

lstsq

scipy.linalg.lstsq(a, b, условие=None, overwrite_a=False, overwrite_b=False, check_finite=True, lapack_driver=None)

Вычислить решение методом наименьших квадратов для уравнения a @ x = b.

Вычислить вектор x такой, что 2-норма |b - A x| минимизируется.

Документация написана в предположении, что аргументы-массивы имеют указанные «основные» формы. Однако аргументы-массивы этой функции могут иметь дополнительные «пакетные» измерения, добавленные перед основной формой. В этом случае массив обрабатывается как пакет низкоразмерных срезов; см. Пакетные линейные операции подробности.

Параметры:

a(M, N) array_like

Массив левой части

b(M,) или (M, K) array_like

Массив правой части

условиеfloat, опционально

Порог для 'малых' сингулярных значений; используется для определения эффективного ранга a. Сингулярные значения меньше cond * largest_singular_value считаются нулевыми.

overwrite_abool, необязательно

Отбросить данные в a (может повысить производительность). По умолчанию False.

overwrite_bbool, необязательно

Отбросить данные в b (может повысить производительность). По умолчанию False.

check_finitebool, необязательно

Проверять ли, что входные матрицы содержат только конечные числа. Отключение может повысить производительность, но может привести к проблемам (сбоям, бесконечному выполнению), если входные данные содержат бесконечности или NaN.

lapack_driverstr, optional

Какой драйвер LAPACK используется для решения задачи наименьших квадратов. Варианты: 'gelsd', 'gelsy', 'gelss'. По умолчанию ('gelsd') является хорошим выбором. Однако, 'gelsy' может быть немного быстрее для многих задач. 'gelss' использовалось исторически. Обычно работает медленно, но использует меньше памяти.

Добавлено в версии 0.17.0.

Возвращает:

x(N,) или (N, K) ndarray

Решение методом наименьших квадратов.

residues(K,) ndarray или float

Квадрат 2-нормы для каждого столбца в b - a x, если M > N и rank(A) == n (возвращает скаляр, если b является одномерным). В противном случае возвращается массив формы (0,).

rankint

Эффективный ранг a.

s(min(M, N),) ndarray или None

Сингулярные значения a. Число обусловленности a является s[0] / s[-1].

Вызывает:

LinAlgError

Если вычисление не сходится.

ValueError

Когда параметры несовместимы.

Смотрите также

scipy.optimize.nnls

линейный метод наименьших квадратов с ограничением неотрицательности

Примечания

Когда 'gelsy' используется как драйвер, residues устанавливается в массив формы (0,) и s всегда None.

Примеры

Попробуйте в вашем браузере!

>>> import numpy as np
>>> from scipy.linalg import lstsq
>>> import matplotlib.pyplot as plt

Предположим, у нас есть следующие данные:

>>> x = np.array([1, 2.5, 3.5, 4, 5, 7, 8.5])
>>> y = np.array([0.3, 1.1, 1.5, 2.0, 3.2, 6.6, 8.6])

Мы хотим подогнать квадратичный полином вида y = a + b*x**2 к этим данным. Сначала формируем "матрицу плана" M с постоянным столбцом из 1 и столбцом, содержащим x**2:

>>> M = x[:, np.newaxis]**[0, 2]
>>> M
array([[  1.  ,   1.  ],
       [  1.  ,   6.25],
       [  1.  ,  12.25],
       [  1.  ,  16.  ],
       [  1.  ,  25.  ],
       [  1.  ,  49.  ],
       [  1.  ,  72.25]])

Мы хотим найти решение методом наименьших квадратов для M.dot(p) = y, где p является вектором длиной 2, содержащим параметры a и b.

>>> p, res, rnk, s = lstsq(M, y)
>>> p
array([ 0.20925829,  0.12013861])

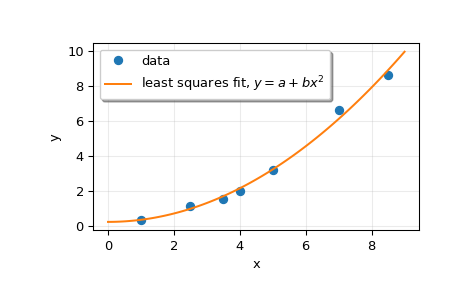
Построить график данных и подобранной кривой.

>>> plt.plot(x, y, 'o', label='data')
>>> xx = np.linspace(0, 9, 101)
>>> yy = p[0] + p[1]*xx**2
>>> plt.plot(xx, yy, label='least squares fit, $y = a + bx^2$')
>>> plt.xlabel('x')
>>> plt.ylabel('y')
>>> plt.legend(framealpha=1, shadow=True)
>>> plt.grid(alpha=0.25)
>>> plt.show()

НазадОткрыть во вкладке