scipy.optimize.

скобка#

scipy.optimize.скобка(функция, xa=0.0, xb=1.0, args=(), grow_limit=110.0, maxiter=1000)[источник]#

Ограничить минимум функции.

Для заданной функции и различных начальных точек выполнить поиск в направлении спуска (определяемом начальными точками) и вернуть три точки, ограничивающие минимум функции.

Параметры:

функциявызываемая функция f(x,*args): Целевая функция для минимизации.
xa, xbfloat, опционально: Начальные точки. По умолчанию xa до 0.0, и xb до 1.0. Локальный минимум не обязательно должен находиться в этом интервале.
argsкортеж, необязательный: Дополнительные аргументы (если присутствуют), передаваемые в функция.
grow_limitfloat, опционально: Максимальный предел роста. По умолчанию: 110.0
maxiterint, необязательный: Максимальное количество итераций для выполнения. По умолчанию 1000.

Возвращает:

xa, xb, xcfloat: Конечные точки интервала.
fa, fb, fcfloat: Значения целевой функции в точках скобки.
funcallsint: Количество выполненных оценок функции.

Вызывает:

BracketError: Если до завершения алгоритма не найдена допустимая скобка. См. примечания для условий допустимой скобки.

Примечания

Алгоритм пытается найти три строго упорядоченные точки (т.е. \(x_a < x_b < x_c\) или \(x_c < x_b < x_a\)) удовлетворяющий \(f(x_b) ≤ f(x_a)\) и \(f(x_b) ≤ f(x_c)\), где одно из неравенств должно быть строго удовлетворено, и все \(x_i\) должен быть конечным.

Примеры

Эта функция может найти выпуклую вниз область функции:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.optimize import bracket
>>> def f(x):
...     return 10*x**2 + 3*x + 5
>>> x = np.linspace(-2, 2)
>>> y = f(x)
>>> init_xa, init_xb = 0.1, 1
>>> xa, xb, xc, fa, fb, fc, funcalls = bracket(f, xa=init_xa, xb=init_xb)
>>> plt.axvline(x=init_xa, color="k", linestyle="--")
>>> plt.axvline(x=init_xb, color="k", linestyle="--")
>>> plt.plot(x, y, "-k")
>>> plt.plot(xa, fa, "bx")
>>> plt.plot(xb, fb, "rx")
>>> plt.plot(xc, fc, "bx")
>>> plt.show()

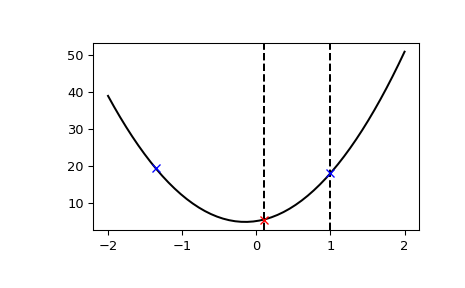
../../_images/scipy-optimize-bracket-1_00_00.png

Обратите внимание, что обе начальные точки находились справа от минимума, и третья точка была найдена в "нисходящем" направлении: направлении, в котором функция, по-видимому, убывала (влево). Конечные точки строго упорядочены, и значение функции в средней точке меньше значений функции в конечных точках; отсюда следует, что минимум должен находиться внутри скобки.