scipy.signal.

bessel

scipy.signal.bessel(N, Wn, btype='low', аналог=False, вывод='ba', norm='фаза', fs=None)

Проектирование цифровых и аналоговых фильтров Бесселя/Томсона.

Спроектируйте цифровой или аналоговый фильтр Бесселя N-го порядка и верните коэффициенты фильтра.

Параметры:

Nint

Порядок фильтра.

Wnarray_like

Скаляр или последовательность длины 2, задающая критические частоты (определенные norm параметр). Для аналоговых фильтров, Wn является угловой частотой (например, рад/с).

Для цифровых фильтров, Wn в тех же единицах, что и fs. По умолчанию, fs составляет 2 полуцикла/сэмпл, поэтому они нормализованы от 0 до 1, где 1 — частота Найквиста. (Wn следовательно, в полуциклах / сэмпл.)

btype{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}, необязательно

Тип фильтра. По умолчанию — 'lowpass'.

аналогbool, необязательно

Если True, возвращает аналоговый фильтр, в противном случае возвращается цифровой фильтр. (См. Примечания.)

вывод{‘ba’, ‘zpk’, ‘sos’}, опционально

Тип вывода: числитель/знаменатель ('ba'), полюс-ноль ('zpk'), или секции второго порядка ('sos'). По умолчанию 'ba'.

norm{‘phase’, ‘delay’, ‘mag’}, опционально

Нормализация критической частоты:

phase

Фильтр нормализован так, что фазовая характеристика достигает середины на угловой (например, рад/с) частоте Wn. Это происходит для как низкочастотных, так и высокочастотных фильтров, так что это случай «согласования фазы».

Асимптоты амплитудной характеристики такие же, как у фильтра Баттерворта того же порядка с частотой среза Wn.

Это значение по умолчанию и соответствует реализации MATLAB.

delay

Фильтр нормализован таким образом, что групповая задержка в полосе пропускания равна 1/Wn (например, секунды). Это «естественный» тип, полученный решением полиномов Бесселя.

mag

Фильтр нормализован так, что амплитуда усиления составляет -3 дБ на угловой частоте Wn.

Добавлено в версии 0.18.0.

fsfloat, опционально

Частота дискретизации цифровой системы.

Добавлено в версии 1.2.0.

Возвращает:

b, aСоздать LinearOperators

Числитель (b) и знаменатель (a) полиномы IIR-фильтра. Возвращается только если output='ba'.

z, p, kndarray, ndarray, float

Нули, полюсы и коэффициент усиления системы передаточной функции фильтра IIR. Возвращается только если output='zpk'.

sosndarray

Представление фильтра IIR в виде звеньев второго порядка. Возвращается только если output='sos'.

Примечания

Также известный как фильтр Томсона, аналоговый фильтр Бесселя имеет максимально плоскую групповую задержку и максимально линейную фазовую характеристику с очень малым выбросом в переходной характеристике. [1]

Фильтр Бесселя по своей природе является аналоговым. Эта функция генерирует цифровые фильтры Бесселя с использованием билинейного преобразования, которое не сохраняет фазовую характеристику аналогового фильтра. Таким образом, оно лишь приблизительно корректно на частотах ниже примерно fs/4. Для получения максимально плоской групповой задержки на более высоких частотах аналоговый фильтр Бесселя должен быть преобразован с использованием методов, сохраняющих фазу.

См. besselap для подробностей реализации и ссылок.

The 'sos' выходной параметр был добавлен в версии 0.16.0.

Ссылки

[1]

Thomson, W.E., “Delay Networks having Maximally Flat Frequency Characteristics”, Proceedings of the Institution of Electrical Engineers, Part III, November 1949, Vol. 96, No. 44, pp. 487-490.

Примеры

Попробуйте в вашем браузере!

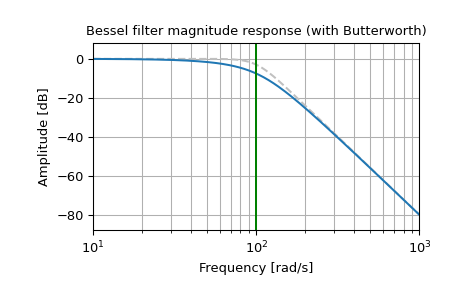
Построение фазо-нормированной частотной характеристики, показывающей связь с частотой среза Баттерворта (зеленая):

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> b, a = signal.butter(4, 100, 'low', analog=True)
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(np.abs(h)), color='silver', ls='dashed')
>>> b, a = signal.bessel(4, 100, 'low', analog=True, norm='phase')
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(np.abs(h)))
>>> plt.title('Bessel filter magnitude response (with Butterworth)')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(100, color='green')  # cutoff frequency
>>> plt.show()

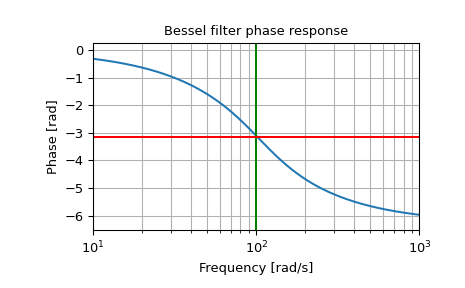
и средняя точка фазы:

>>> plt.figure()
>>> plt.semilogx(w, np.unwrap(np.angle(h)))
>>> plt.axvline(100, color='green')  # cutoff frequency
>>> plt.axhline(-np.pi, color='red')  # phase midpoint
>>> plt.title('Bessel filter phase response')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Phase [rad]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.show()

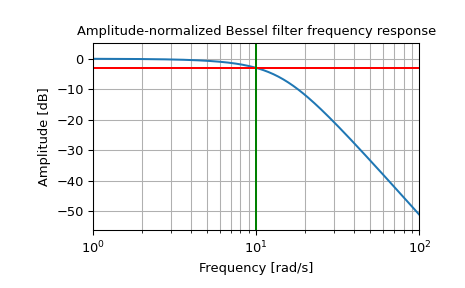
Постройте нормированную по амплитуде частотную характеристику, показывающую срез -3 дБ:

>>> b, a = signal.bessel(3, 10, 'low', analog=True, norm='mag')
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(np.abs(h)))
>>> plt.axhline(-3, color='red')  # -3 dB magnitude
>>> plt.axvline(10, color='green')  # cutoff frequency
>>> plt.title('Amplitude-normalized Bessel filter frequency response')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.show()

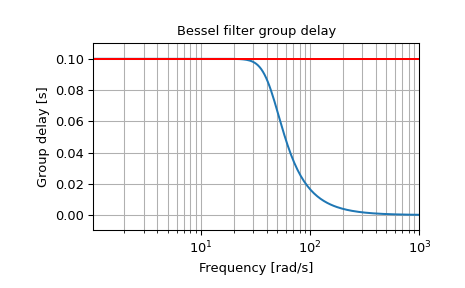
Построить фильтр с нормализованной задержкой, показывающий максимально плоскую групповую задержку на 0.1 секунды:

>>> b, a = signal.bessel(5, 1/0.1, 'low', analog=True, norm='delay')
>>> w, h = signal.freqs(b, a)
>>> plt.figure()
>>> plt.semilogx(w[1:], -np.diff(np.unwrap(np.angle(h)))/np.diff(w))
>>> plt.axhline(0.1, color='red')  # 0.1 seconds group delay
>>> plt.title('Bessel filter group delay')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Group delay [s]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.show()

НазадОткрыть во вкладке