scipy.signal.

bilinear_zpk#

scipy.signal.bilinear_zpk(z, p, k, fs)[источник]#

Вернуть цифровой IIR-фильтр из аналогового с использованием билинейного преобразования.

Преобразовать набор полюсов и нулей из аналоговой s-плоскости в цифровую z-плоскость с использованием метода Тастина, который подставляет 2*fs*(z-1) / (z+1) для s, сохраняя форму частотной характеристики.

Параметры:

zarray_like: Нули передаточной функции аналогового фильтра.
parray_like: Полюсы передаточной функции аналогового фильтра.
kfloat: Коэффициент усиления системы аналогового фильтра передаточной функции.
fsfloat: Частота дискретизации, как обычная частота (например, герцы). В этой функции не выполняется предварительная коррекция частоты.

Возвращает:

zndarray: Нули передаточной функции преобразованного цифрового фильтра.
pndarray: Полюсы передаточной функции преобразованного цифрового фильтра.
kfloat: Коэффициент усиления системы преобразованного цифрового фильтра.

Смотрите также

lp2lp_zpk, lp2hp_zpk, lp2bp_zpk, lp2bs_zpk
bilinear

Примечания

Добавлено в версии 1.1.0.

Примеры

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

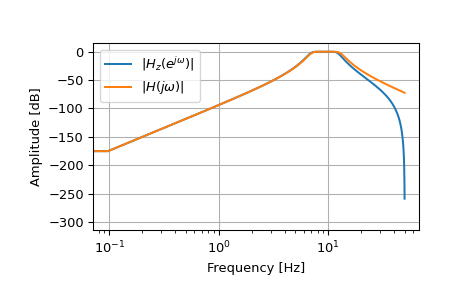
>>> fs = 100
>>> bf = 2 * np.pi * np.array([7, 13])
>>> filts = signal.lti(*signal.butter(4, bf, btype='bandpass', analog=True,
...                                   output='zpk'))
>>> filtz = signal.lti(*signal.bilinear_zpk(filts.zeros, filts.poles,
...                                         filts.gain, fs))
>>> wz, hz = signal.freqz_zpk(filtz.zeros, filtz.poles, filtz.gain)
>>> ws, hs = signal.freqs_zpk(filts.zeros, filts.poles, filts.gain,
...                           worN=fs*wz)
>>> plt.semilogx(wz*fs/(2*np.pi), 20*np.log10(np.abs(hz).clip(1e-15)),
...              label=r'$|H_z(e^{j \omega})|$')
>>> plt.semilogx(wz*fs/(2*np.pi), 20*np.log10(np.abs(hs).clip(1e-15)),
...              label=r'$|H(j \omega)|$')
>>> plt.legend()
>>> plt.xlabel('Frequency [Hz]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.grid(True)

../../_images/scipy-signal-bilinear_zpk-1.png