билинейный#
- scipy.signal.билинейный(b, a, fs=1.0)[источник]#
Вычислить цифровой БИХ-фильтр из аналоговой передаточной функции с использованием билинейного преобразования.
- Параметры:
- barray_like
Коэффициенты полинома числителя аналоговой передаточной функции в виде комплексного или вещественного одномерного массива.
- aarray_like
Коэффициенты полинома знаменателя аналоговой передаточной функции в виде одномерного массива комплексных или действительных значений.
- fsfloat
Частота дискретизации, как обычная частота (например, герцы). Предварительная коррекция не выполняется в этой функции.
- Возвращает:
- betandarray
Коэффициенты полинома числителя цифровой передаточной функции в виде комплексного или вещественного одномерного массива.
- alphandarray
Коэффициенты полинома знаменателя цифровой передаточной функции в виде комплексного или вещественного одномерного массива.
Смотрите также
lp2lp,lp2hp,lp2bp,lp2bs,bilinear_zpk
Примечания
Параметры \(b = [b_0, \ldots, b_Q]\) и \(a = [a_0, \ldots, a_P]\) являются одномерными массивами длины \(Q+1\) и \(P+1\). Они определяют аналоговую передаточную функцию
\[H_a(s) = \frac{b_0 s^Q + b_1 s^{Q-1} + \cdots + b_Q}{ a_0 s^P + a_1 s^{P-1} + \cdots + a_P}\ .\]Билинейное преобразование [1] применяется путём подстановки
\[s = \kappa \frac{z-1}{z+1}\ , \qquad \kappa := 2 f_s\ ,\]в \(H_a(s)\), с \(f_s\) будучи частотой дискретизации. Это приводит к цифровой передаточной функции в \(z\)-domain
\[H_d(z) = \frac{b_0 \left(\kappa \frac{z-1}{z+1}\right)^Q + b_1 \left(\kappa \frac{z-1}{z+1}\right)^{Q-1} + \cdots + b_Q}{ a_0 \left(\kappa \frac{z-1}{z+1}\right)^P + a_1 \left(\kappa \frac{z-1}{z+1}\right)^{P-1} + \cdots + a_P}\ .\]Это выражение можно упростить, умножив числитель и знаменатель на \((z+1)^N\), с \(N=\max(P, Q)\). Это позволяет \(H_d(z)\) чтобы быть переформулированным как
\[\begin{split}& & \frac{b_0 \big(\kappa (z-1)\big)^Q (z+1)^{N-Q} + b_1 \big(\kappa (z-1)\big)^{Q-1} (z+1)^{N-Q+1} + \cdots + b_Q(z+1)^N}{ a_0 \big(\kappa (z-1)\big)^P (z+1)^{N-P} + a_1 \big(\kappa (z-1)\big)^{P-1} (z+1)^{N-P+1} + \cdots + a_P(z+1)^N}\\ &=:& \frac{\beta_0 + \beta_1 z^{-1} + \cdots + \beta_N z^{-N}}{ \alpha_0 + \alpha_1 z^{-1} + \cdots + \alpha_N z^{-N}}\ .\end{split}\]Это уравнение, реализованное для выполнения билинейного преобразования. Обратите внимание, что для больших \(f_s\), \(\kappa^Q\) или \(\kappa^P\) может вызвать числовое переполнение для достаточно больших \(P\) или \(Q\).
Ссылки
Примеры
Следующий пример показывает частотную характеристику аналогового полосового фильтра и соответствующего цифрового фильтра, полученного с использованием билинейного преобразования:
>>> from scipy import signal >>> import matplotlib.pyplot as plt >>> import numpy as np ... >>> fs = 100 # sampling frequency >>> om_c = 2 * np.pi * np.array([7, 13]) # corner frequencies >>> bb_s, aa_s = signal.butter(4, om_c, btype='bandpass', analog=True, output='ba') >>> bb_z, aa_z = signal.bilinear(bb_s, aa_s, fs) ... >>> w_z, H_z = signal.freqz(bb_z, aa_z) # frequency response of digitial filter >>> w_s, H_s = signal.freqs(bb_s, aa_s, worN=w_z*fs) # analog filter response ... >>> f_z, f_s = w_z * fs / (2*np.pi), w_s / (2*np.pi) >>> Hz_dB, Hs_dB = (20*np.log10(np.abs(H_).clip(1e-10)) for H_ in (H_z, H_s)) >>> fg0, ax0 = plt.subplots() >>> ax0.set_title("Frequency Response of 4-th order Bandpass Filter") >>> ax0.set(xlabel='Frequency $f$ in Hertz', ylabel='Magnitude in dB', ... xlim=[f_z[1], fs/2], ylim=[-200, 2]) >>> ax0.semilogx(f_z, Hz_dB, alpha=.5, label=r'$|H_z(e^{j 2 \pi f})|$') >>> ax0.semilogx(f_s, Hs_dB, alpha=.5, label=r'$|H_s(j 2 \pi f)|$') >>> ax0.legend() >>> ax0.grid(which='both', axis='x') >>> ax0.grid(which='major', axis='y') >>> plt.show()
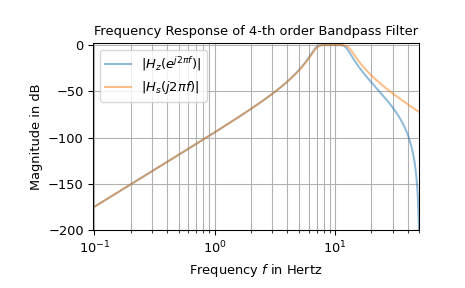
Разница в более высоких частотах, показанная на графике, вызвана эффектом, называемым «частотным искажением». [1] описывает метод, называемый «предварительным искажением», для уменьшения этих отклонений.