scipy.signal.

cont2discrete#

scipy.signal.cont2discrete(система, dt, метод='zoh', alpha=None)[источник]#

Преобразование непрерывной системы в дискретную систему пространства состояний.

Параметры:
системакортеж, описывающий систему, или экземпляр lti

Следующее дает количество элементов в кортеже и их интерпретацию:

  • 1: (экземпляр lti)

  • 2: (num, den)

  • 3: (нули, полюсы, коэффициент усиления)

  • 4: (A, B, C, D)

dtfloat

Шаг дискретизации по времени.

методstr, optional

Какой метод использовать:

  • gbt: обобщённое билинейное преобразование

  • билинейный: аппроксимация Тастина ("gbt" с alpha=0.5)

  • euler: метод Эйлера (или прямых разностей) (“gbt” с alpha=0)

  • backward_diff: Обратное дифференцирование (“gbt” с alpha=1.0)

  • zoh: нулевого порядка (по умолчанию)

  • foh: удержание первого порядка (versionadded: 1.3.0)

  • impulse: эквивалентная импульсная характеристика (versionadded: 1.3.0)

alphafloat в пределах [0, 1], опционально

Параметр веса обобщённого билинейного преобразования, который должен указываться только с method="gbt" и игнорируется в противном случае

Возвращает:
sysdкортеж, содержащий дискретную систему

В зависимости от типа ввода, вывод будет иметь форму

  • (num, den, dt) для ввода передаточной функции

  • (нули, полюса, коэффициент усиления, dt) для ввода нулей-полюсов-усиления

  • (A, B, C, D, dt) для ввода системы в пространстве состояний

Примечания

По умолчанию процедура использует метод Zero-Order Hold (zoh) для выполнения преобразования. Альтернативно может использоваться обобщённое билинейное преобразование, которое включает распространённую билинейную аппроксимацию Тастина, метод Эйлера или метод обратных разностей.

Метод Zero-Order Hold (zoh) основан на [1], обобщённое билинейное приближение основано на [2] и [3], метод First-Order Hold (foh) основан на [4].

Ссылки

[3]

G. Zhang, X. Chen, и T. Chen, Цифровое перепроектирование с помощью обобщенного билинейного преобразования, Int. J. Control, т. 82, № 4, стр. 741-754, 2009. (https://www.mypolyuweb.hk/~magzhang/Research/ZCC09_IJC.pdf)

[4]

G. F. Franklin, J. D. Powell, и M. L. Workman, Digital control of dynamic systems, 3rd ed. Menlo Park, Calif: Addison-Wesley, pp. 204-206, 1998.

Примеры

Мы можем преобразовать непрерывную систему в пространстве состояний в дискретную:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import cont2discrete, lti, dlti, dstep

Определите непрерывную систему в пространстве состояний.

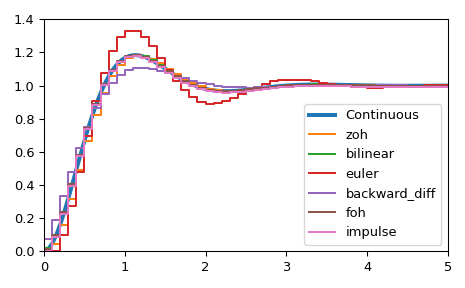
>>> A = np.array([[0, 1],[-10., -3]])
>>> B = np.array([[0],[10.]])
>>> C = np.array([[1., 0]])
>>> D = np.array([[0.]])
>>> l_system = lti(A, B, C, D)
>>> t, x = l_system.step(T=np.linspace(0, 5, 100))
>>> fig, ax = plt.subplots()
>>> ax.plot(t, x, label='Continuous', linewidth=3)

Преобразуйте его в дискретную систему пространства состояний несколькими методами.

>>> dt = 0.1
>>> for method in ['zoh', 'bilinear', 'euler', 'backward_diff', 'foh', 'impulse']:
...    d_system = cont2discrete((A, B, C, D), dt, method=method)
...    s, x_d = dstep(d_system)
...    ax.step(s, np.squeeze(x_d), label=method, where='post')
>>> ax.axis([t[0], t[-1], x[0], 1.4])
>>> ax.legend(loc='best')
>>> fig.tight_layout()
>>> plt.show()
../../_images/scipy-signal-cont2discrete-1.png
На этой странице