scipy.signal.

place_poles#

scipy.signal.place_poles(A, B, полюса, метод='YT', rtol=0.001, maxiter=30)[источник]#

Вычислить K так, чтобы собственные значения (A - dot(B, K))=полюсам.

K — это матрица усиления, такая как система, описываемая линейной системой AX+BU будет иметь свои полюса замкнутого контура, т.е. собственные значения A - B*K, как можно ближе к запрошенным в полюсах.

Поддерживаются системы SISO, MISO и MIMO.

Параметры:
A, Bndarray

Представление линейной системы в пространстве состояний AX + BU.

полюсаarray_like

Желаемые вещественные полюса и/или комплексно-сопряженные полюса. Комплексные полюса поддерживаются только с method="YT" (по умолчанию).

метод: {'YT', 'KNV0'}, опционально

Какой метод выбрать для нахождения матрицы усиления K. Один из:

  • 'YT': Yang Tits

  • 'KNV0': Метод обновления Каутского, Николса, Ван Дорена 0

См. Ссылки и Примечания для подробностей об алгоритмах.

rtol: float, опционально

После каждой итерации определитель собственных векторов A - B*K сравнивается с предыдущим значением, когда относительная ошибка между этими двумя значениями становится меньше rtol алгоритм останавливается. По умолчанию 1e-3.

maxiter: int, optional

Максимальное количество итераций для вычисления матрицы усиления. По умолчанию 30.

Возвращает:
full_state_feedbackОбъект Bunch
full_state_feedback состоит из:
gain_matrix1-D ndarray

Матрица замкнутого контура K такая, что собственные значения A-BK максимально близки к требуемым полюсам.

вычисленные_полюса1-D ndarray

Полюса, соответствующие A-BK сортируется сначала по вещественным полюсам в порядке возрастания, затем по комплексно-сопряженным в лексикографическом порядке.

requested_poles1-D ndarray

Полюса, которые алгоритм должен был разместить, отсортированы как выше, они могут отличаться от достигнутых.

X2-D ndarray

Матрица передачи, такая как X * diag(poles) = (A - B*K)*X (см. Примечания)

rtolfloat

Относительная точность, достигнутая на det(X) (см. Примечания). rtol будет NaN, если возможно решить систему diag(poles) = (A - B*K), или 0, когда алгоритмы оптимизации не могут ничего сделать, т.е. когда B.shape[1] == 1.

nb_iterint

Количество итераций, выполненных до сходимости. nb_iter будет NaN, если возможно решить систему diag(poles) = (A - B*K), или 0, когда алгоритмы оптимизации не могут ничего сделать, т.е. когда B.shape[1] == 1.

Примечания

Tits and Yang (YT), [2] Статья является обновлением оригинальной статьи Kautsky et al. (KNV) [1]. KNV использует обновления ранга 1 для нахождения передаточной матрицы X такой, что X * diag(poles) = (A - B*K)*X, тогда как YT использует обновления ранга-2. Это в среднем даёт более устойчивые решения (см. [2] стр. 21-22), кроме того, алгоритм YT поддерживает комплексные полюса, тогда как KNV не поддерживает в своей оригинальной версии. Здесь реализован только метод обновления 0, предложенный KNV, отсюда и название 'KNV0'.

KNV, расширенный до комплексных полюсов, используется в Matlab place функция, YT распространяется под несвободной лицензией Slicot под названием robpole. Неясно и не задокументировано, как KNV0 был расширен для комплексных полюсов (Tits и Yang утверждают на странице 14 своей статьи, что их метод не может быть использован для расширения KNV на комплексные полюса), поэтому только YT поддерживает их в этой реализации.

Поскольку решение задачи размещения полюсов не единственно для MIMO систем, оба метода начинают с пробной передаточной матрицы, которая изменяется различными способами для увеличения её определителя. Оба метода доказали сходимость к устойчивому решению, однако в зависимости от способа выбора начальной передаточной матрицы они сходятся к разным решениям, и поэтому нет абсолютно никакой гарантии, что использование 'KNV0' даст результаты, аналогичные Matlab или любой другой реализации этих алгоритмов.

Используя метод по умолчанию 'YT' должно быть нормально в большинстве случаев; 'KNV0' предоставляется только потому, что требуется для 'YT' в некоторых конкретных случаях. Кроме того 'YT' дает в среднем более надежные результаты, чем 'KNV0' когда abs(det(X)) используется как показатель устойчивости.

[2] доступен как технический отчет по следующему URL: https://hdl.handle.net/1903/5598

Ссылки

[1] (1,2)

Дж. Каутски, Н.К. Николс и П. ван Дорен, «Робастное назначение полюсов в линейной обратной связи по состоянию», International Journal of Control, Том 41, стр. 1129-1155, 1985.

[2] (1,2,3)

A.L. Tits и Y. Yang, «Globally convergent algorithms for robust pole assignment by state feedback», IEEE Transactions on Automatic Control, Vol. 41, pp. 1432-1452, 1996.

Примеры

Простой пример, демонстрирующий размещение вещественных полюсов с использованием алгоритмов KNV и YT. Это пример номер 1 из раздела 4 ссылки на публикацию KNV ([1]):

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt

>>> A = np.array([[ 1.380,  -0.2077,  6.715, -5.676  ],
...               [-0.5814, -4.290,   0,      0.6750 ],
...               [ 1.067,   4.273,  -6.654,  5.893  ],
...               [ 0.0480,  4.273,   1.343, -2.104  ]])
>>> B = np.array([[ 0,      5.679 ],
...               [ 1.136,  1.136 ],
...               [ 0,      0,    ],
...               [-3.146,  0     ]])
>>> P = np.array([-0.2, -0.5, -5.0566, -8.6659])

Теперь вычислите K методом KNV 0, методом YT по умолчанию и методом YT с принудительным выполнением 100 итераций алгоритма и выведите некоторые результаты после каждого вызова.

>>> fsf1 = signal.place_poles(A, B, P, method='KNV0')
>>> fsf1.gain_matrix
array([[ 0.20071427, -0.96665799,  0.24066128, -0.10279785],
       [ 0.50587268,  0.57779091,  0.51795763, -0.41991442]])

>>> fsf2 = signal.place_poles(A, B, P)  # uses YT method
>>> fsf2.computed_poles
array([-8.6659, -5.0566, -0.5   , -0.2   ])

>>> fsf3 = signal.place_poles(A, B, P, rtol=-1, maxiter=100)
>>> fsf3.X
array([[ 0.52072442+0.j, -0.08409372+0.j, -0.56847937+0.j,  0.74823657+0.j],
       [-0.04977751+0.j, -0.80872954+0.j,  0.13566234+0.j, -0.29322906+0.j],
       [-0.82266932+0.j, -0.19168026+0.j, -0.56348322+0.j, -0.43815060+0.j],
       [ 0.22267347+0.j,  0.54967577+0.j, -0.58387806+0.j, -0.40271926+0.j]])

Абсолютное значение определителя X — хороший показатель для проверки устойчивости результатов, как 'KNV0' и 'YT' нацелены на максимизацию его. Ниже сравнение устойчивости результатов выше:

>>> abs(np.linalg.det(fsf1.X)) < abs(np.linalg.det(fsf2.X))
True
>>> abs(np.linalg.det(fsf2.X)) < abs(np.linalg.det(fsf3.X))
True

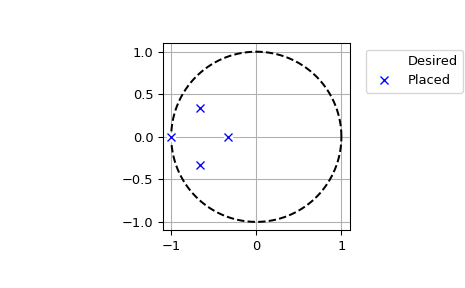
Теперь простой пример для комплексных полюсов:

>>> A = np.array([[ 0,  7/3.,  0,   0   ],
...               [ 0,   0,    0,  7/9. ],
...               [ 0,   0,    0,   0   ],
...               [ 0,   0,    0,   0   ]])
>>> B = np.array([[ 0,  0 ],
...               [ 0,  0 ],
...               [ 1,  0 ],
...               [ 0,  1 ]])
>>> P = np.array([-3, -1, -2-1j, -2+1j]) / 3.
>>> fsf = signal.place_poles(A, B, P, method='YT')

Мы можем построить желаемые и вычисленные полюсы в комплексной плоскости:

>>> t = np.linspace(0, 2*np.pi, 401)
>>> plt.plot(np.cos(t), np.sin(t), 'k--')  # unit circle
>>> plt.plot(fsf.requested_poles.real, fsf.requested_poles.imag,
...          'wo', label='Desired')
>>> plt.plot(fsf.computed_poles.real, fsf.computed_poles.imag, 'bx',
...          label='Placed')
>>> plt.grid()
>>> plt.axis('image')
>>> plt.axis([-1.1, 1.1, -1.1, 1.1])
>>> plt.legend(bbox_to_anchor=(1.05, 1), loc=2, numpoints=1)
../../_images/scipy-signal-place_poles-1.png
На этой странице