scipy.signal.

correlate

scipy.signal.correlate(in1, in2, mode='full', метод='auto')

Вычислить взаимную корреляцию двух N-мерных массивов.

Взаимная корреляция in1 и in2, с размером вывода, определяемым mode аргумент.

Параметры:

in1array_like

Первый вход.

in2array_like

Второй вход. Должен иметь то же количество измерений, что и in1.

modestr {‘full’, ‘valid’, ‘same’}, необязательный

Строка, указывающая размер вывода:

full

Выходные данные представляют собой полную дискретную линейную взаимную корреляцию входных данных. (По умолчанию)

valid

Выходные данные состоят только из тех элементов, которые не зависят от дополнения нулями. В режиме 'valid' либо in1 или in2 должен быть как минимум таким же большим, как другой, по каждому измерению.

same

Выходные данные имеют тот же размер, что и in1, центрированный относительно вывода 'full'.

методstr {'auto', 'direct', 'fft'}, optional

Строка, указывающая, какой метод использовать для расчета корреляции.

direct

Корреляция определяется непосредственно из сумм, по определению корреляции.

fft

Быстрое преобразование Фурье используется для более быстрого выполнения корреляции (доступно только для числовых массивов).

auto

Автоматически выбирает прямой или метод Фурье на основе оценки того, какой быстрее (по умолчанию). См. convolve Подробности см. в примечаниях.

Добавлено в версии 0.19.0.

Возвращает:

correlateмассив

N-мерный массив, содержащий подмножество дискретной линейной кросс-корреляции in1 с in2.

Смотрите также

choose_conv_method

содержит больше документации по метод.

correlation_lags

вычисляет массив индексов задержки/смещения для одномерной взаимной корреляции.

Примечания

Корреляция z двух d-мерных массивов x и y определяется как:

z[...,k,...] = sum[..., i_l, ...] x[..., i_l,...] * conj(y[..., i_l - k,...])

Таким образом, если x и y являются 1-D массивами и z = correlate(x, y, 'full') затем

\[z[k] = \sum_{l=0}^{N-1} x_l \, y_{l-k}^{*}\]

для \(k = -(M-1), \dots, (N-1)\), где \(N\) является длиной x, \(M\) является длиной y, и \(y_m = 0\) когда \(m\) находится вне допустимого диапазона \([0, M-1]\). Размер \(z\) является \(N + M - 1\) и \(y^*\) обозначает комплексное сопряжение \(y\).

method='fft' работает только для числовых массивов, так как полагается на fftconvolve. В некоторых случаях (т.е., массивы объектов или когда округление целых чисел может привести к потере точности), method='direct' всегда используется.

При использовании mode='same' с входными данными четной длины, выходы correlate и correlate2d различаются: между ними существует смещение на 1 индекс.

Примеры

Попробуйте в вашем браузере!

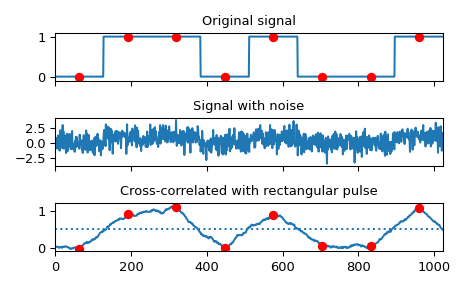
Реализуйте согласованный фильтр с использованием взаимной корреляции для восстановления сигнала, прошедшего через зашумлённый канал.

>>> import numpy as np
>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()

>>> sig = np.repeat([0., 1., 1., 0., 1., 0., 0., 1.], 128)
>>> sig_noise = sig + rng.standard_normal(len(sig))
>>> corr = signal.correlate(sig_noise, np.ones(128), mode='same') / 128

>>> clock = np.arange(64, len(sig), 128)
>>> fig, (ax_orig, ax_noise, ax_corr) = plt.subplots(3, 1, sharex=True)
>>> ax_orig.plot(sig)
>>> ax_orig.plot(clock, sig[clock], 'ro')
>>> ax_orig.set_title('Original signal')
>>> ax_noise.plot(sig_noise)
>>> ax_noise.set_title('Signal with noise')
>>> ax_corr.plot(corr)
>>> ax_corr.plot(clock, corr[clock], 'ro')
>>> ax_corr.axhline(0.5, ls=':')
>>> ax_corr.set_title('Cross-correlated with rectangular pulse')
>>> ax_orig.margins(0, 0.1)
>>> fig.tight_layout()
>>> plt.show()

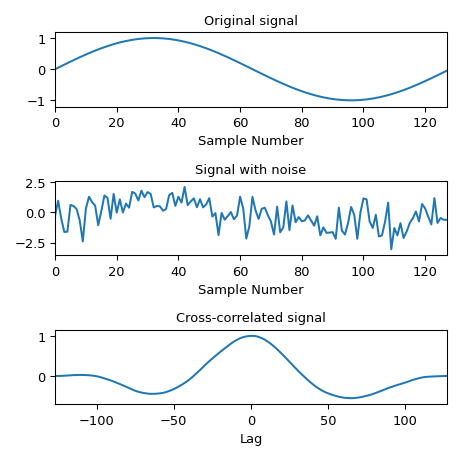
Вычислить кросс-корреляцию зашумленного сигнала с исходным сигналом.

>>> x = np.arange(128) / 128
>>> sig = np.sin(2 * np.pi * x)
>>> sig_noise = sig + rng.standard_normal(len(sig))
>>> corr = signal.correlate(sig_noise, sig)
>>> lags = signal.correlation_lags(len(sig), len(sig_noise))
>>> corr /= np.max(corr)

>>> fig, (ax_orig, ax_noise, ax_corr) = plt.subplots(3, 1, figsize=(4.8, 4.8))
>>> ax_orig.plot(sig)
>>> ax_orig.set_title('Original signal')
>>> ax_orig.set_xlabel('Sample Number')
>>> ax_noise.plot(sig_noise)
>>> ax_noise.set_title('Signal with noise')
>>> ax_noise.set_xlabel('Sample Number')
>>> ax_corr.plot(lags, corr)
>>> ax_corr.set_title('Cross-correlated signal')
>>> ax_corr.set_xlabel('Lag')
>>> ax_orig.margins(0, 0.1)
>>> ax_noise.margins(0, 0.1)
>>> ax_corr.margins(0, 0.1)
>>> fig.tight_layout()
>>> plt.show()

НазадОткрыть во вкладке