scipy.signal.

dbode#

scipy.signal.dbode(система, w=None, n=100)[источник]#

Вычислить данные амплитуды и фазы Боде для дискретной системы.

Параметры:

системаdlti | кортеж

Экземпляр класса LTI dlti или кортеж, описывающий систему. Количество элементов в кортеже определяет интерпретацию. Т.е.:

system: Экземпляр класса LTI dlti. Обратите внимание, что производные экземпляры, такие как экземпляры TransferFunction, ZerosPolesGain, или StateSpace, также допускаются.
(num, den, dt): Рациональный полином, как описано в TransferFunction. Коэффициенты полиномов должны быть указаны в порядке убывания степеней, например, z² + 3z + 5 должно быть представлено как [1, 3, 5].
(zeros, poles, gain, dt): Форма нулей, полюсов и коэффициента усиления, как описано в ZerosPolesGain.
(A, B, C, D, dt): Форма пространства состояний, как описано в StateSpace.

warray_like, необязательный

Массив частот, нормализованных к частоте Найквиста π, т.е. имеющих единицу радиан/отсчёт. Данные амплитуды и фазы вычисляются для каждого значения в этом массиве. Если не задано, будет вычислен разумный набор.

nint, необязательный

Количество частотных точек для вычисления, если w не задан. n частоты логарифмически распределены в интервале, выбранном так, чтобы включить влияние полюсов и нулей системы.

Возвращает:

w1D ndarray: Массив частот, нормированных к частоте Найквиста, равной np.pi/dt с dt является интервалом выборки для система параметр. Единица измерения — рад/с, предполагая dt в секундах.
mag1D ndarray: Массив величин в дБ
фаза1D ndarray: Фазовый массив в градусах

Смотрите также

dfreqresp, dlti, TransferFunction, ZerosPolesGain, StateSpace

Примечания

Эта функция является удобной оболочкой вокруг dfreqresp для извлечения амплитуды и фазы из вычисленного комплексного значения амплитуды частотной характеристики.

Добавлено в версии 0.18.0.

Примеры

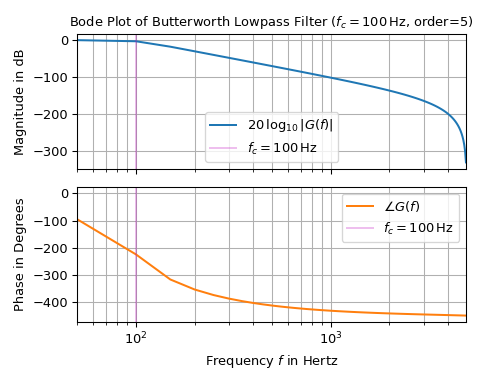
Следующий пример показывает, как создать диаграмму Боде для фильтра Баттерворта 5-го порядка с частотой среза 100 Гц:

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy import signal
...
>>> T = 1e-4  # sampling interval in s
>>> f_c, o = 1e2, 5  # corner frequency in Hz (i.e., -3 dB value) and filter order
>>> bb, aa = signal.butter(o, f_c, 'lowpass', fs=1/T)
...
>>> w, mag, phase = signal.dbode((bb, aa, T))
>>> w /= 2*np.pi  # convert unit of frequency into Hertz
...
>>> fg, (ax0, ax1) = plt.subplots(2, 1, sharex='all', figsize=(5, 4),
...                               tight_layout=True)
>>> ax0.set_title("Bode Plot of Butterworth Lowpass Filter " +
...               rf"($f_c={f_c:g}\,$Hz, order={o})")
>>> ax0.set_ylabel(r"Magnitude in dB")
>>> ax1.set(ylabel=r"Phase in Degrees",
...         xlabel="Frequency $f$ in Hertz", xlim=(w[1], w[-1]))
>>> ax0.semilogx(w, mag, 'C0-', label=r"$20\,\log_{10}|G(f)|$")  # Magnitude plot
>>> ax1.semilogx(w, phase, 'C1-', label=r"$\angle G(f)$")  # Phase plot
...
>>> for ax_ in (ax0, ax1):
...     ax_.axvline(f_c, color='m', alpha=0.25, label=rf"${f_c=:g}\,$Hz")
...     ax_.grid(which='both', axis='x')  # plot major & minor vertical grid lines
...     ax_.grid(which='major', axis='y')
...     ax_.legend()
>>> plt.show()