scipy.signal.

dfreqresp#

scipy.signal.dfreqresp(система, w=None, n=10000, целый=False)[источник]#

Вычислите частотную характеристику дискретной системы.

Параметры:

системаdlti | кортеж

Экземпляр класса LTI dlti или кортеж, описывающий систему. Количество элементов в кортеже определяет интерпретацию. Т.е.:

system: Экземпляр класса LTI dlti. Обратите внимание, что производные экземпляры, такие как экземпляры TransferFunction, ZerosPolesGain, или StateSpace, также допускаются.
(num, den, dt): Рациональный полином, как описано в TransferFunction. Коэффициенты полиномов должны быть указаны в порядке убывания степеней, например, z² + 3z + 5 должно быть представлено как [1, 3, 5].
(zeros, poles, gain, dt): Форма нулей, полюсов и коэффициента усиления, как описано в ZerosPolesGain.
(A, B, C, D, dt): Форма пространства состояний, как описано в StateSpace.

warray_like, необязательный

Массив частот (в радианах/сэмпл). Данные о величине и фазе рассчитываются для каждого значения в этом массиве. Если не задан, будет рассчитан разумный набор.

nint, необязательный

Количество частотных точек для вычисления, если w не задан. n частоты логарифмически распределены в интервале, выбранном так, чтобы включить влияние полюсов и нулей системы.

целыйbool, необязательно

Обычно, если ‘w’ не задан, частоты вычисляются от 0 до частоты Найквиста, пи радиан/образец (верхняя половина единичной окружности). Если целый равно True, вычислять частоты от 0 до 2*pi радиан/отсчёт.

Возвращает:

w1D ndarray: Массив частот [радианы/сэмпл]
H1D ndarray: Массив значений комплексной амплитуды

Примечания

Если (num, den) передано для system, коэффициенты как для числителя, так и для знаменателя должны быть указаны в порядке убывания степени (например, z^2 + 3z + 5 будет представлен как [1, 3, 5]).

Добавлено в версии 0.18.0.

Примеры

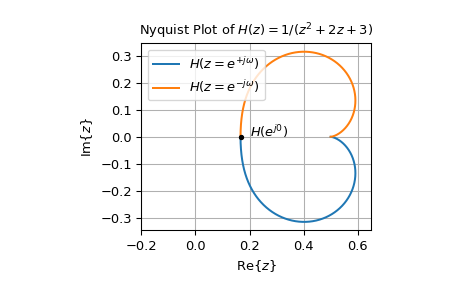
Следующий пример генерирует диаграмму Найквиста передаточной функции \(H(z) = \frac{1}{z^2 + 2z + 3}\) с временем выборки 0.05 секунд:

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> sys = signal.TransferFunction([1], [1, 2, 3], dt=0.05)  # construct H(z)
>>> w, H = signal.dfreqresp(sys)
...
>>> fig0, ax0 = plt.subplots()
>>> ax0.plot(H.real, H.imag, label=r"$H(z=e^{+j\omega})$")
>>> ax0.plot(H.real, -H.imag, label=r"$H(z=e^{-j\omega})$")
>>> ax0.set_title(r"Nyquist Plot of $H(z) = 1 / (z^2 + 2z + 3)$")
>>> ax0.set(xlabel=r"$\text{Re}\{z\}$", ylabel=r"$\text{Im}\{z\}$",
...         xlim=(-0.2, 0.65), aspect='equal')
>>> ax0.plot(H[0].real, H[0].imag, 'k.')  # mark H(exp(1j*w[0]))
>>> ax0.text(0.2, 0, r"$H(e^{j0})$")
>>> ax0.grid(True)
>>> ax0.legend()
>>> plt.show()

../../_images/scipy-signal-dfreqresp-1.png