scipy.signal.

ellip#

scipy.signal.ellip(N, rp, rs, Wn, btype='low', аналог=False, вывод='ba', fs=None)[источник]#

Эллиптический (Кауэра) цифровой и аналоговый проектирование фильтров.

Спроектировать цифровой или аналоговый эллиптический фильтр N-го порядка и вернуть коэффициенты фильтра.

Параметры:

Nint

Порядок фильтра.

rpfloat

Максимально допустимая пульсация ниже единичного усиления в полосе пропускания. Задаётся в децибелах как положительное число.

rsfloat

Минимальное ослабление, требуемое в полосе задерживания. Указывается в децибелах как положительное число.

Wnarray_like

Скаляр или последовательность длины 2, задающая критические частоты. Для эллиптических фильтров это точка в переходной полосе, в которой усиление впервые падает ниже -rp.

Для цифровых фильтров, Wn в тех же единицах, что и fs. По умолчанию, fs составляет 2 полуцикла/сэмпл, поэтому они нормализованы от 0 до 1, где 1 — частота Найквиста. (Wn следовательно, в полуциклах / сэмпл.)

Для аналоговых фильтров, Wn является угловой частотой (например, рад/с).

btype{‘lowpass’, ‘highpass’, ‘bandpass’, ‘bandstop’}, необязательно

Тип фильтра. По умолчанию 'lowpass'.

аналогbool, необязательно

Если True, возвращает аналоговый фильтр, в противном случае возвращается цифровой фильтр.

вывод{‘ba’, ‘zpk’, ‘sos’}, опционально

Тип вывода: числитель/знаменатель ('ba'), полюс-ноль ('zpk') или секции второго порядка ('sos'). По умолчанию 'ba' для обратной совместимости, но 'sos' следует использовать для фильтрации общего назначения.

fsfloat, опционально

Частота дискретизации цифровой системы.

Добавлено в версии 1.2.0.

Возвращает:

b, aСоздать LinearOperators: Числитель (b) и знаменатель (a) полиномы IIR-фильтра. Возвращается только если output='ba'.
z, p, kndarray, ndarray, float: Нули, полюсы и коэффициент усиления системы передаточной функции фильтра IIR. Возвращается только если output='zpk'.
sosndarray: Представление фильтра IIR в виде звеньев второго порядка. Возвращается только если output='sos'.

Смотрите также

ellipord, ellipap

Примечания

Также известные как фильтры Кауэра или Золотарева, эллиптический фильтр максимизирует скорость перехода между полосой пропускания и полосой задерживания частотной характеристики, за счёт пульсаций в обеих и увеличения звона в переходной характеристике.

Поскольку rp приближается к 0, эллиптический фильтр становится фильтром типа Чебышева II (cheby2). Как rs приближается к 0, он становится фильтром типа Чебышева I (cheby1). По мере приближения обоих к 0, он становится фильтром Баттерворта (butter).

Равноволновая полоса пропускания имеет N максимумов или минимумов (например, фильтр 5-го порядка имеет 3 максимума и 2 минимума). Следовательно, коэффициент усиления по постоянному току равен единице для фильтров нечётного порядка или -rp дБ для фильтров чётного порядка.

The 'sos' выходной параметр был добавлен в версии 0.16.0.

Примеры

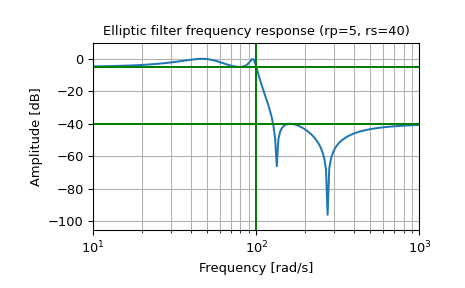
Спроектировать аналоговый фильтр и построить его частотную характеристику, показывая критические точки:

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> b, a = signal.ellip(4, 5, 40, 100, 'low', analog=True)
>>> w, h = signal.freqs(b, a)
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.title('Elliptic filter frequency response (rp=5, rs=40)')
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(100, color='green') # cutoff frequency
>>> plt.axhline(-40, color='green') # rs
>>> plt.axhline(-5, color='green') # rp
>>> plt.show()

../../_images/scipy-signal-ellip-1_00_00.png

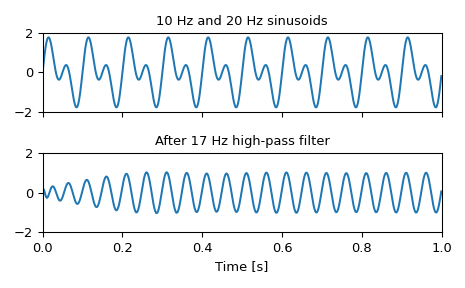
Сгенерировать сигнал, состоящий из 10 Гц и 20 Гц, с частотой дискретизации 1 кГц

>>> t = np.linspace(0, 1, 1000, False)  # 1 second
>>> sig = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t)
>>> fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True)
>>> ax1.plot(t, sig)
>>> ax1.set_title('10 Hz and 20 Hz sinusoids')
>>> ax1.axis([0, 1, -2, 2])

Спроектируйте цифровой высокочастотный фильтр на 17 Гц для удаления тона 10 Гц и примените его к сигналу. (Рекомендуется использовать формат секций второго порядка при фильтрации, чтобы избежать численной ошибки с передаточной функцией (ba) формат):

>>> sos = signal.ellip(8, 1, 100, 17, 'hp', fs=1000, output='sos')
>>> filtered = signal.sosfilt(sos, sig)
>>> ax2.plot(t, filtered)
>>> ax2.set_title('After 17 Hz high-pass filter')
>>> ax2.axis([0, 1, -2, 2])
>>> ax2.set_xlabel('Time [s]')
>>> plt.tight_layout()
>>> plt.show()

../../_images/scipy-signal-ellip-1_01_00.png