scipy.signal.

огибающая#

scipy.signal.огибающая(z, bp_in=(1, None), *, n_out=None, квадрат=False, остаток='lowpass', ось=-1)[источник]#

Вычисление огибающей вещественного или комплексного сигнала.

Параметры:

zndarray: Вещественный или комплексный входной сигнал, который предполагается состоящим из n выборки и имея интервал выборки T. z также может быть многомерным массивом с осью времени, определенной через ось.
bp_intuple[int | None, int | None], опционально: 2-кортеж, определяющий частотную полосу bp_in[0]:bp_in[1] входного фильтра. Граничные частоты указываются как целые кратные 1/(n*T) с -n//2 <= bp_in[0] < bp_in[1] <= (n+1)//2 являясь допустимым диапазоном частот. None записи заменены на -n//2 или (n+1)//2 соответственно. Значение по умолчанию (1, None) удаляет среднее значение, а также компоненты отрицательной частоты.
n_outint | None, optional: Если не None выходные данные будут передискретизированы до n_out образцов. Значение по умолчанию None устанавливает выходную длину равной входной z.
квадратbool, необязательно: Если установлено, возвращается квадрат огибающей. Полоса пропускания квадрата огибающей часто меньше полосы пропускания не возведённой в квадрат огибающей из-за нелинейной природы используемой функции абсолютного значения. Т.е. встроенная функция квадратного корня обычно создаёт дополнительные гармоники. По умолчанию False.
остатокLiteral[‘lowpass’, ‘all’, None], опционально: Эта опция определяет, какой тип остатка, т.е. часть сигнала, которую удаляет входной полосовой фильтр, возвращается. 'all' возвращает всё, кроме содержимого частотной полосы bp_in[0]:bp_in[1], 'lowpass' возвращает содержимое частотной полосы < bp_in[0]. Если None тогда возвращается только огибающая. По умолчанию: 'lowpass'.
осьint, необязательный: Ось z по которому вычисляется огибающая. По умолчанию последняя ось.

Возвращает:

ndarray: Если параметр остаток является None затем массив z_env с той же формой, что и входные данные z возвращается, содержащий его огибающую. В противном случае массив с формой (2, *z.shape), содержащий массивы z_env и z_res, сложенные вдоль первой оси, возвращаются. Это позволяет распаковку, т.е., z_env, z_res = envelope(z, residual='all'). Остаток z_res содержит часть сигнала, которую входной полосовой фильтр удалил, в зависимости от параметра остаток. Обратите внимание, что для вещественных сигналов возвращается вещественный остаток. Следовательно, компоненты отрицательной частоты bp_in игнорируются.

Смотрите также

hilbert: Вычислите аналитический сигнал с помощью преобразования Гильберта.

Примечания

Любой комплекснозначный сигнал \(z(t)\) может быть описана вещественной мгновенной амплитудой \(a(t)\) и вещественную мгновенную фазу \(\phi(t)\), т.е., \(z(t) = a(t) \exp\!\big(j \phi(t)\big)\). Огибающая определяется как абсолютное значение амплитуды \(|a(t)| = |z(t)|\), что одновременно является абсолютным значением сигнала. Следовательно, \(|a(t)|\) «огибает» класс всех сигналов с амплитудой \(a(t)\) и произвольная фаза \(\phi(t)\). Для вещественных сигналов, \(x(t) = a(t) \cos\!\big(\phi(t)\big)\) это аналогичная формулировка. Следовательно, \(|a(t)|\) может быть определено путем преобразования \(x(t)\) в аналитический сигнал \(z_a(t)\) с помощью преобразования Гильберта, т.е., \(z_a(t) = a(t) \cos\!\big(\phi(t)\big) + j a(t) \sin\!\big(\phi(t) \big)\), что даёт комплексный сигнал с той же огибающей \(|a(t)|\).

Реализация основана на вычислении БПФ входного сигнала и последующем выполнении необходимых операций в пространстве Фурье. Следовательно, необходимо учитывать типичные ограничения БПФ:

Предполагается, что сигнал периодический. Разрывы между началом и концом сигнала могут привести к нежелательным результатам из-за явления Гиббса.
БПФ работает медленно, если длина сигнала является простым числом или очень большой. Также требования к памяти обычно выше, чем у реализации на основе КИХ/БИХ-фильтров.
Частотный интервал 1 / (n*T) для частот среза полосового фильтра соответствует частотам, создаваемым scipy.fft.fftfreq(len(z), T).

Если огибающая комплекснозначного сигнала z без полосовой фильтрации требуется, т.е. bp_in=(None, None), тогда огибающая соответствует абсолютному значению. Следовательно, более эффективно использовать np.abs(z) вместо этой функции.

Хотя вычисление огибающей на основе аналитического сигнала [1] является естественным методом для вещественных сигналов, другие методы также часто используются. Самой популярной альтернативой, вероятно, является так называемый «квадратичный» детектор огибающей и его родственные методы [2]. Они не всегда вычисляют правильный результат для всех видов сигналов, но обычно корректны и, как правило, вычислительно более эффективны для большинства видов узкополосных сигналов. Определение огибающей, представленное здесь, является общим, когда важны мгновенная амплитуда и фаза (например, как описано в [3]). Существуют также другие концепции, основанные на общей математической идее оболочки [4]: Прагматичный подход заключается в определении всех верхних и нижних пиков сигнала и использовании сплайн-интерполяции для определения кривых [5].

Ссылки

[1]

"Аналитический сигнал", Википедия, https://en.wikipedia.org/wiki/Analytic_signal

[2]

Лайонс, Ричард, «Цифровое детектирование огибающей: хорошее, плохое и ужасное», IEEE Signal Processing Magazine 34.4 (2017): 183-187. PDF

[3]

T.G. Kincaid, “The complex representation of signals.”, TIS R67# MH5, General Electric Co. (1966). PDF

[4]

“Огибающая (математика)”, Википедия, https://en.wikipedia.org/wiki/Envelope_(mathematics)

[5]

Yang, Yanli. “A signal theoretic approach for envelope analysis of real-valued signals.” IEEE Access 5 (2017): 5623-5630. PDF

Примеры

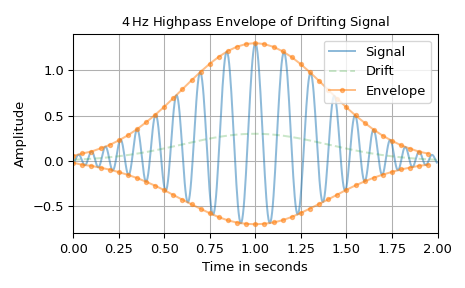
Следующий график иллюстрирует огибающую сигнала с переменной частотой и низкочастотным дрейфом. Чтобы отделить дрейф от огибающей, используется фильтр верхних частот 4 Гц. Низкочастотный остаток входного полосового фильтра используется для определения асимметричной верхней и нижней границ, охватывающих сигнал. Из-за гладкости результирующей огибающей она прореживается с 500 до 40 отсчётов. Обратите внимание, что мгновенная амплитуда a_x и вычисленная огибающая x_env не являются абсолютно идентичными. Это связано с тем, что сигнал не является идеально периодическим, а также с существованием некоторого спектрального перекрытия x_carrier и x_drift. Следовательно, они не могут быть полностью разделены полосовым фильтром.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal.windows import gaussian
>>> from scipy.signal import envelope
...
>>> n, n_out = 500, 40  # number of signal samples and envelope samples
>>> T = 2 / n  # sampling interval for 2 s duration
>>> t = np.arange(n) * T  # time stamps
>>> a_x = gaussian(len(t), 0.4/T)  # instantaneous amplitude
>>> phi_x = 30*np.pi*t + 35*np.cos(2*np.pi*0.25*t)  # instantaneous phase
>>> x_carrier = a_x * np.cos(phi_x)
>>> x_drift = 0.3 * gaussian(len(t), 0.4/T)  # drift
>>> x = x_carrier + x_drift
...
>>> bp_in = (int(4 * (n*T)), None)  # 4 Hz highpass input filter
>>> x_env, x_res = envelope(x, bp_in, n_out=n_out)
>>> t_out = np.arange(n_out) * (n / n_out) * T
...
>>> fg0, ax0 = plt.subplots(1, 1, tight_layout=True)
>>> ax0.set_title(r"$4\,$Hz Highpass Envelope of Drifting Signal")
>>> ax0.set(xlabel="Time in seconds", xlim=(0, n*T), ylabel="Amplitude")
>>> ax0.plot(t, x, 'C0-', alpha=0.5, label="Signal")
>>> ax0.plot(t, x_drift, 'C2--', alpha=0.25, label="Drift")
>>> ax0.plot(t_out, x_res+x_env, 'C1.-', alpha=0.5, label="Envelope")
>>> ax0.plot(t_out, x_res-x_env, 'C1.-', alpha=0.5, label=None)
>>> ax0.grid(True)
>>> ax0.legend()
>>> plt.show()

../../_images/scipy-signal-envelope-1_00_00.png

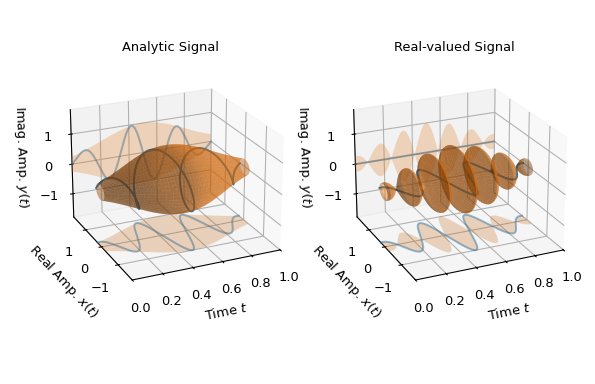
Второй пример дает геометрическую интерпретацию огибающей для комплекснозначных сигналов: следующие два графика показывают комплекснозначный сигнал как синюю 3d-траекторию и огибающую как оранжевую круглую трубку с переменным диаметром, т.е., как \(|a(t)| \exp(j\rho(t))\), с \(\rho(t)\in[-\pi,\pi]\). Также проекция в 2d-плоскости действительных и мнимых координат траектории и трубки изображена. Каждая точка комплекснозначного сигнала касается поверхности трубки.

Левый график показывает аналитический сигнал, т.е. разность фаз между мнимой и действительной частями всегда составляет 90 градусов, что приводит к спиральной траектории. Видно, что в этом случае действительная часть также имеет ожидаемую огибающую, т.е. представляет абсолютное значение мгновенной амплитуды.

Правый график показывает действительную часть этого аналитического сигнала, интерпретируемого как комплекснозначный сигнал, т.е. имеющего нулевую мнимую часть. Там результирующая огибающая не такая гладкая, как в аналитическом случае, и мгновенная амплитуда в действительной плоскости не восстанавливается. Если z_re был передан как вещественный сигнал, т.е. как z_re = z.real вместо z_re = z.real + 0j, результат был бы идентичен левому графику. Причина в том, что вещественные сигналы интерпретируются как вещественная часть комплексного аналитического сигнала.

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from scipy.signal.windows import gaussian
>>> from scipy.signal import envelope
...
>>> n, T = 1000, 1/1000  # number of samples and sampling interval
>>> t = np.arange(n) * T  # time stamps for 1 s duration
>>> f_c = 3  # Carrier frequency for signal
>>> z = gaussian(len(t), 0.3/T) * np.exp(2j*np.pi*f_c*t)  # analytic signal
>>> z_re = z.real + 0j  # complex signal with zero imaginary part
...
>>> e_a, e_r = (envelope(z_, (None, None), residual=None) for z_ in (z, z_re))
...
>>> # Generate grids to visualize envelopes as 2d and 3d surfaces:
>>> E2d_t, E2_amp = np.meshgrid(t, [-1, 1])
>>> E2d_1 = np.ones_like(E2_amp)
>>> E3d_t, E3d_phi = np.meshgrid(t, np.linspace(-np.pi, np.pi, 300))
>>> ma = 1.8  # maximum axis values in real and imaginary direction
...
>>> fg0 = plt.figure(figsize=(6.2, 4.))
>>> ax00 = fg0.add_subplot(1, 2, 1, projection='3d')
>>> ax01 = fg0.add_subplot(1, 2, 2, projection='3d', sharex=ax00,
...                        sharey=ax00, sharez=ax00)
>>> ax00.set_title("Analytic Signal")
>>> ax00.set(xlim=(0, 1), ylim=(-ma, ma), zlim=(-ma, ma))
>>> ax01.set_title("Real-valued Signal")
>>> for z_, e_, ax_ in zip((z, z.real), (e_a, e_r), (ax00, ax01)):
...     ax_.set(xlabel="Time $t$", ylabel="Real Amp. $x(t)$",
...             zlabel="Imag. Amp. $y(t)$")
...     ax_.plot(t, z_.real, 'C0-', zs=-ma, zdir='z', alpha=0.5, label="Real")
...     ax_.plot_surface(E2d_t, e_*E2_amp, -ma*E2d_1, color='C1', alpha=0.25)
...     ax_.plot(t, z_.imag, 'C0-', zs=+ma, zdir='y', alpha=0.5, label="Imag.")
...     ax_.plot_surface(E2d_t, ma*E2d_1, e_*E2_amp, color='C1', alpha=0.25)
...     ax_.plot(t, z_.real, z_.imag, 'C0-', label="Signal")
...     ax_.plot_surface(E3d_t, e_*np.cos(E3d_phi), e_*np.sin(E3d_phi),
...                      color='C1', alpha=0.5, shade=True, label="Envelope")
...     ax_.view_init(elev=22.7, azim=-114.3)
>>> fg0.subplots_adjust(left=0.08, right=0.97, wspace=0.15)
>>> plt.show()

../../_images/scipy-signal-envelope-1_01_00.png