scipy.signal.

гильберт#

scipy.signal.гильберт(x, N=None, ось=-1)[источник]#

FFT-вычисление аналитического сигнала.

Аналитический сигнал вычисляется путём фильтрации отрицательных частот и удвоения амплитуд положительных частот в области БПФ. Мнимая часть результата — это преобразование Гильберта вещественного входного сигнала.

Преобразование выполняется вдоль последней оси по умолчанию.

Параметры:

xarray_like: Данные сигнала. Должны быть вещественными.
Nint, необязательный: Количество компонент Фурье. По умолчанию: x.shape[axis]
осьint, необязательный: Ось, вдоль которой выполняется преобразование. По умолчанию: -1.

Возвращает:

xandarray: Аналитический сигнал x, каждого 1-D массива вдоль ось

Смотрите также

envelope: Вычислить огибающую вещественного или комплексного сигнала.

Примечания

Аналитический сигнал x_a(t) вещественного сигнала x(t) может быть выражен как [1]

\[x_a = F^{-1}(F(x) 2U) = x + i y\ ,\]

где F является преобразованием Фурье, U функция единичного скачка, и y преобразование Гильберта от x. [2]

Другими словами, отрицательная половина спектра частот обнуляется, превращая вещественный сигнал в комплексный сигнал. Преобразованный по Гильберту сигнал может быть получен из np.imag(hilbert(x)), и исходный сигнал из np.real(hilbert(x)).

Ссылки

[1]

Википедия, «Аналитический сигнал». https://en.wikipedia.org/wiki/Analytic_signal

[2]

Википедия, «Преобразование Гильберта». https://en.wikipedia.org/wiki/Hilbert_transform

[3]

Леон Коэн, «Анализ время-частота», 1995. Глава 2.

[4]

Алан В. Оппенгейм, Рональд В. Шафер. Цифровая обработка сигналов, Третье издание, 2009. Глава 12. ISBN 13: 978-1292-02572-8

Примеры

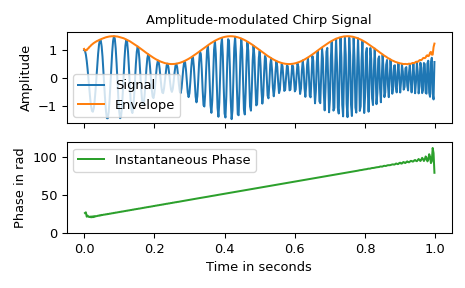
В этом примере мы используем преобразование Гильберта для определения амплитудной огибающей и мгновенной частоты амплитудно-модулированного сигнала.

Давайте создадим чирп, частота которого увеличивается с 20 Гц до 100 Гц, и применим амплитудную модуляцию:

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.signal import hilbert, chirp
...
>>> duration, fs = 1, 400  # 1 s signal with sampling frequency of 400 Hz
>>> t = np.arange(int(fs*duration)) / fs  # timestamps of samples
>>> signal = chirp(t, 20.0, t[-1], 100.0)
>>> signal *= (1.0 + 0.5 * np.sin(2.0*np.pi*3.0*t) )

Огибающая амплитуды задается модулем аналитического сигнала. Мгновенная частота может быть получена путем дифференцирования мгновенной фазы по времени. Мгновенная фаза соответствует фазовому углу аналитического сигнала.

>>> analytic_signal = hilbert(signal)
>>> amplitude_envelope = np.abs(analytic_signal)
>>> instantaneous_phase = np.unwrap(np.angle(analytic_signal))
>>> instantaneous_frequency = np.diff(instantaneous_phase) / (2.0*np.pi) * fs
...
>>> fig, (ax0, ax1) = plt.subplots(nrows=2, sharex='all', tight_layout=True)
>>> ax0.set_title("Amplitude-modulated Chirp Signal")
>>> ax0.set_ylabel("Amplitude")
>>> ax0.plot(t, signal, label='Signal')
>>> ax0.plot(t, amplitude_envelope, label='Envelope')
>>> ax0.legend()
>>> ax1.set(xlabel="Time in seconds", ylabel="Phase in rad", ylim=(0, 120))
>>> ax1.plot(t[1:], instantaneous_frequency, 'C2-', label='Instantaneous Phase')
>>> ax1.legend()
>>> plt.show()

../../_images/scipy-signal-hilbert-1.png