scipy.signal.

firwin_2d

scipy.signal.firwin_2d(hsize, window, *, fc=None, fs=2, круговой=False, pass_zero=True, scale=True)

Проектирование 2D КИХ-фильтров с использованием оконного метода.

Эта функция вычисляет коэффициенты двумерного КИХ-фильтра. Фильтр сепарабелен с линейной фазой; он будет спроектирован как произведение двух одномерных фильтров с размерами, определенными hsize. Кроме того, он может создавать приблизительно циркулярно-симметричные 2-D окна.

Параметры:

hsizeкортеж или список длины 2

Длины фильтра в каждом измерении. hsize[0] указывает количество коэффициентов в направлении строки и hsize[1] определяет количество коэффициентов в направлении столбца.

windowкортеж или список длины 2 или строка

Желаемое окно для использования с каждым 1D фильтром или единый тип окна для создания циклически симметричных 2-D окон. Каждый элемент должен быть строкой или кортежем строки и значений параметров. См. get_window для списка окон и требуемых параметров.

fcfloat или 1-D array_like, опционально

Частота среза фильтра в тех же единицах, что и fs. Это определяет частоту, на которой усиление фильтра падает примерно до -6 дБ (половинная мощность) в фильтре нижних или верхних частот. Для многополосных фильтров, fc может быть массивом частот среза (т.е. границ полос) в диапазоне [0, fs/2], где каждая полоса задается парами. Требуется, если круговой равно False.

fsfloat, опционально

Частота дискретизации сигнала. По умолчанию 2.

круговойbool, необязательно

Создавать ли циклически симметричное 2-D окно. По умолчанию False.

pass_zero{True, False, ‘bandpass’, ‘lowpass’, ‘highpass’, ‘bandstop’}, опционально

Этот параметр напрямую передаётся в firwin для каждой скалярной частотной оси. Следовательно, если True, коэффициент усиления по постоянному току, т.е. усиление на частоте (0, 0), равно 1. Если False, коэффициент усиления постоянного тока равен 0 на частоте (0, 0), если круговой является True. Если круговой является False частоты (0, f1) и (f0, 0) будут иметь усиление 0. Это также может быть строковый аргумент для желаемого типа фильтра (эквивалентно btype в функциях проектирования БИХ-фильтров).

scalebool, необязательно

Этот параметр напрямую передаётся в firwin для каждой скалярной оси частот. Установить в True для масштабирования коэффициентов, чтобы частотная характеристика была точно равна единице на определенной частоте на одной частотной оси. Эта частота либо:

• 0 (постоянная составляющая), если первая полоса пропускания начинается с 0 (т.е. pass_zero равен True)

• fs/2 (частота Найквиста), если первый полосовой фильтр заканчивается на fs/2 (т.е. фильтр является однополосным фильтром верхних частот); центр первой полосы пропускания в противном случае

Возвращает:

filter_2d(hsize[0], hsize[1]) ndarray

Коэффициенты 2D FIR-фильтра.

Вызывает:

ValueError

• Если hsize и window не являются кортежами или списками из 2 элементов.

• Если порог равно None, когда круговой равно True.

• Если порог находится вне диапазона [0, fs/2] и круговой является False.

• Если любой из элементов в window не распознаются.

RuntimeError

Если firwin не сходится при проектировании фильтра.

Смотрите также

firwin

Проектирование FIR-фильтров с использованием оконного метода для одномерных массивов.

get_window

Возвращает окно заданной длины и типа.

Примеры

Попробуйте в вашем браузере!

Сгенерировать фильтр низких частот 5x5 с частотой среза 0.1:

>>> import numpy as np
>>> from scipy.signal import get_window
>>> from scipy.signal import firwin_2d
>>> hsize = (5, 5)
>>> window = (("kaiser", 5.0), ("kaiser", 5.0))
>>> fc = 0.1
>>> filter_2d = firwin_2d(hsize, window, fc=fc)
>>> filter_2d
array([[0.00025366, 0.00401662, 0.00738617, 0.00401662, 0.00025366],
       [0.00401662, 0.06360159, 0.11695714, 0.06360159, 0.00401662],
       [0.00738617, 0.11695714, 0.21507283, 0.11695714, 0.00738617],
       [0.00401662, 0.06360159, 0.11695714, 0.06360159, 0.00401662],
       [0.00025366, 0.00401662, 0.00738617, 0.00401662, 0.00025366]])

Сгенерировать циклически симметричный 5x5 фильтр низких частот с окном Хэмминга:

>>> filter_2d = firwin_2d((5, 5), 'hamming', fc=fc, circular=True)
>>> filter_2d
array([[-0.00020354, -0.00020354, -0.00020354, -0.00020354, -0.00020354],
       [-0.00020354,  0.01506844,  0.09907658,  0.01506844, -0.00020354],
       [-0.00020354,  0.09907658, -0.00020354,  0.09907658, -0.00020354],
       [-0.00020354,  0.01506844,  0.09907658,  0.01506844, -0.00020354],
       [-0.00020354, -0.00020354, -0.00020354, -0.00020354, -0.00020354]])

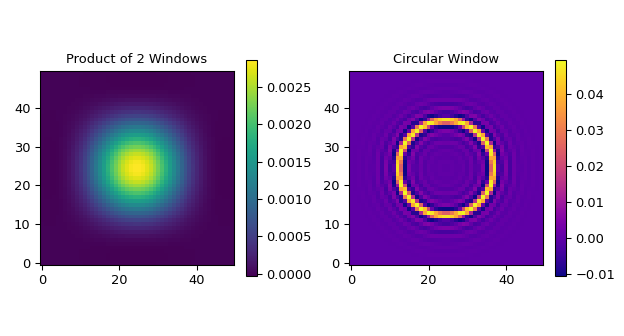
Создать графики, сравнивающие произведение двух одномерных фильтров с круговым симметричным фильтром:

>>> import matplotlib.pyplot as plt
>>> hsize, fc = (50, 50), 0.05
>>> window = (("kaiser", 5.0), ("kaiser", 5.0))
>>> filter0_2d = firwin_2d(hsize, window, fc=fc)
>>> filter1_2d = firwin_2d((50, 50), 'hamming', fc=fc, circular=True)
...
>>> fg, (ax0, ax1) = plt.subplots(1, 2, tight_layout=True, figsize=(6.5, 3.5))
>>> ax0.set_title("Product of 2 Windows")
>>> im0 = ax0.imshow(filter0_2d, cmap='viridis', origin='lower', aspect='equal')
>>> fg.colorbar(im0, ax=ax0, shrink=0.7)
>>> ax1.set_title("Circular Window")
>>> im1 = ax1.imshow(filter1_2d, cmap='plasma', origin='lower', aspect='equal')
>>> fg.colorbar(im1, ax=ax1, shrink=0.7)
>>> plt.show()

НазадОткрыть во вкладке