scipy.signal.

freqs#

scipy.signal.freqs(b, a, worN=200, plot=None)[источник]#

Вычислить частотную характеристику аналогового фильтра.

Для числителя M-го порядка b и знаменатель N-го порядка a аналогового фильтра, вычислите его частотную характеристику:

        b[0]*(jw)**M + b[1]*(jw)**(M-1) + ... + b[M]
H(w) = ----------------------------------------------
        a[0]*(jw)**N + a[1]*(jw)**(N-1) + ... + a[N]

Параметры:

barray_like: Числитель линейного фильтра.
aarray_like: Знаменатель линейного фильтра.
worN{None, int, array_like}, optional: Если None, то вычисляется на 200 частотах вокруг интересных частей кривой отклика (определяемых расположением полюсов и нулей). Если задано одно целое число, то вычисляется на таком количестве частот. В противном случае вычисляется отклик на заданных угловых частотах (например, рад/с) в worN.
plotвызываемый объект, необязательный: Вызываемый объект, принимающий два аргумента. Если задан, возвращаемые параметры w и h передаются в plot. Полезно для построения частотной характеристики внутри freqs.

Возвращает:

wndarray: Угловые частоты, на которых h было вычислено.
hndarray: Частотная характеристика.

Смотрите также

freqz: Вычислить частотную характеристику цифрового фильтра.

Примечания

Использование функции "plot" Matplotlib в качестве вызываемого объекта для plot дает неожиданные результаты, этот график показывает действительную часть комплексной передаточной функции, а не амплитуду. Попробуйте lambda w, h: plot(w, abs(h)).

Примеры

>>> from scipy.signal import freqs, iirfilter
>>> import numpy as np

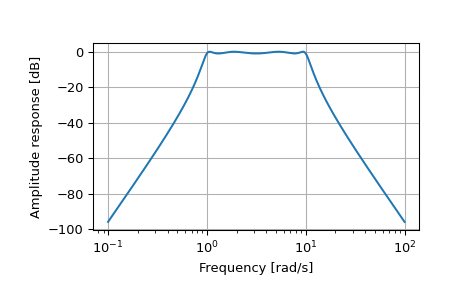
>>> b, a = iirfilter(4, [1, 10], 1, 60, analog=True, ftype='cheby1')

>>> w, h = freqs(b, a, worN=np.logspace(-1, 2, 1000))

>>> import matplotlib.pyplot as plt
>>> plt.semilogx(w, 20 * np.log10(abs(h)))
>>> plt.xlabel('Frequency [rad/s]')
>>> plt.ylabel('Amplitude response [dB]')
>>> plt.grid(True)
>>> plt.show()