scipy.signal.

gammatone

scipy.signal.gammatone(freq, ftype, порядок=None, numtaps=None, fs=None)

Проектирование гамматоновых фильтров.

Эта функция вычисляет коэффициенты КИХ или БИХ гамматонового цифрового фильтра [1].

Параметры:

freqfloat

Центральная частота фильтра (выраженная в тех же единицах, что и fs).

ftype{‘fir’, ‘iir’}

Тип фильтра, генерируемого функцией. Если 'fir', функция сгенерирует FIR-фильтр гамма-тона N-го порядка. Если 'iir', функция сгенерирует цифровой IIR-фильтр 8-го порядка, смоделированный как фильтр гамма-тона 4-го порядка.

порядокint, необязательный

Порядок фильтра. Используется только когда ftype='fir'. По умолчанию 4 для моделирования человеческой слуховой системы. Должно быть между 0 и 24.

numtapsint, необязательный

Длина фильтра. Используется только когда ftype='fir'. По умолчанию fs*0.015 if fs больше 1000, 15 если fs меньше или равно 1000.

fsfloat, опционально

Частота дискретизации сигнала. freq должно быть между 0 и fs/2. По умолчанию 2.

Возвращает:

b, aСоздать LinearOperators

Числитель (b) и знаменатель (a) полиномы фильтра.

Вызывает:

ValueError

Если freq меньше или равна 0 или больше или равна fs/2, если ftype не является ‘fir’ или ‘iir’, если порядок меньше или равно 0 или больше 24, когда ftype='fir'

Смотрите также

firwin

iirfilter

Ссылки

[1]

Slaney, Malcolm, «Эффективная реализация банка слуховых фильтров Паттерсона-Холдсворта», технический отчёт Apple Computer 35, 1993, стр.3-8, 34-39.

Примеры

Попробуйте в вашем браузере!

16-выборочный фильтр Гамматон 4-го порядка с центром на 440 Гц

>>> from scipy import signal
>>> signal.gammatone(440, 'fir', numtaps=16, fs=16000)
(array([ 0.00000000e+00,  2.22196719e-07,  1.64942101e-06,  4.99298227e-06,
    1.01993969e-05,  1.63125770e-05,  2.14648940e-05,  2.29947263e-05,
    1.76776931e-05,  2.04980537e-06, -2.72062858e-05, -7.28455299e-05,
   -1.36651076e-04, -2.19066855e-04, -3.18905076e-04, -4.33156712e-04]),
   [1.0])

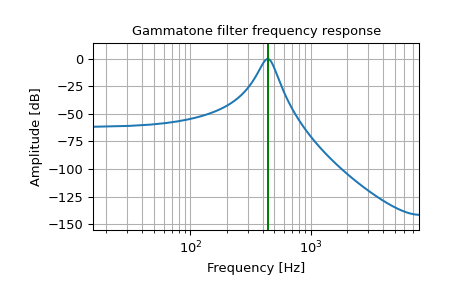
IIR гамматоновый фильтр с центром на 440 Гц

>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> fc, fs = 440, 16000
>>> b, a = signal.gammatone(fc, 'iir', fs=fs)
>>> w, h = signal.freqz(b, a)
>>> plt.plot(w * fs / (2 * np.pi), 20 * np.log10(abs(h)))
>>> plt.xscale('log')
>>> plt.title('Gammatone filter frequency response')
>>> plt.xlabel('Frequency [Hz]')
>>> plt.ylabel('Amplitude [dB]')
>>> plt.margins(0, 0.1)
>>> plt.grid(which='both', axis='both')
>>> plt.axvline(fc, color='green') # cutoff frequency
>>> plt.show()

НазадОткрыть во вкладке