freqz_zpk#
- scipy.signal.freqz_zpk(z, p, k, worN=512, целый=False, fs=6.283185307179586)[источник]#
Вычислите частотную характеристику цифрового фильтра в форме ZPK.
Имея нули, полюсы и коэффициент усиления цифрового фильтра, вычислите его частотную характеристику:
\(H(z)=k \prod_i (z - Z[i]) / \prod_j (z - P[j])\)
где \(k\) является усиление, \(Z\) являются zeros и \(P\) являются полюса.
- Параметры:
- zarray_like
Нули линейного фильтра
- parray_like
Полюса линейного фильтра
- kскаляр
Коэффициент усиления линейного фильтра
- worN{None, int, array_like}, optional
Если указано одно целое число, то вычисления производятся на указанном количестве частот (по умолчанию N=512).
Если передан array_like, вычислить отклик на заданных частотах. Они в тех же единицах, что и fs.
- целыйbool, необязательно
Обычно частоты вычисляются от 0 до частоты Найквиста, fs/2 (верхняя половина единичной окружности). Если целый если True, вычислять частоты от 0 до fs. Игнорируется, если w является array_like.
- fsfloat, опционально
Частота дискретизации цифровой системы. По умолчанию 2*pi радиан/отсчёт (так что w находится в диапазоне от 0 до pi).
Добавлено в версии 1.2.0.
- Возвращает:
- wndarray
Частоты, на которых h было вычислено, в тех же единицах, что и fs. По умолчанию, w нормализован в диапазон [0, pi) (радиан/образец).
- hndarray
Частотная характеристика в виде комплексных чисел.
Смотрите также
Примечания
Добавлено в версии 0.19.0.
Примеры
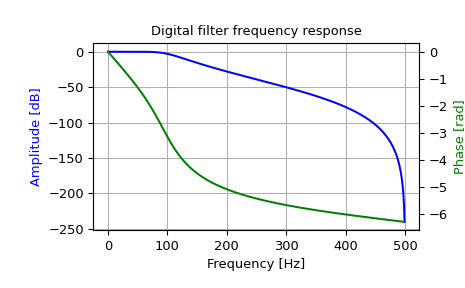
Спроектируйте цифровой фильтр Баттерворта 4-го порядка с частотой среза 100 Гц в системе с частотой дискретизации 1000 Гц и постройте частотную характеристику:
>>> import numpy as np >>> from scipy import signal >>> z, p, k = signal.butter(4, 100, output='zpk', fs=1000) >>> w, h = signal.freqz_zpk(z, p, k, fs=1000)
>>> import matplotlib.pyplot as plt >>> fig = plt.figure() >>> ax1 = fig.add_subplot(1, 1, 1) >>> ax1.set_title('Digital filter frequency response')
>>> ax1.plot(w, 20 * np.log10(abs(h)), 'b') >>> ax1.set_ylabel('Amplitude [dB]', color='b') >>> ax1.set_xlabel('Frequency [Hz]') >>> ax1.grid(True)
>>> ax2 = ax1.twinx() >>> phase = np.unwrap(np.angle(h)) >>> ax2.plot(w, phase, 'g') >>> ax2.set_ylabel('Phase [rad]', color='g')
>>> plt.axis('tight') >>> plt.show()