scipy.signal.

iircomb

scipy.signal.iircomb(w0, Q, ftype='notch', fs=2.0, *, pass_zero=False)

Спроектировать IIR гребенчатый фильтр с подавлением или усилением.

Гребенчатый фильтр с вырезанием состоит из регулярно расположенных полосно-заграждающих фильтров с узкой полосой пропускания (высоким добротностью). Каждый из них подавляет узкую полосу частот и оставляет остальную часть спектра почти неизменной.

Пиковый гребенчатый фильтр состоит из регулярно расположенных полосовых фильтров с узкой полосой пропускания (высоким добротным фактором). Каждый из них отсекает компоненты вне узкой полосы частот.

Параметры:

w0float

Основная частота гребенчатого фильтра (расстояние между его пиками). Она должна равномерно делить частоту дискретизации. Если fs указан, это в тех же единицах, что и fs. По умолчанию это нормированный скаляр, который должен удовлетворять 0 < w0 < 1, с w0 = 1 соответствующая половине частоты дискретизации.

Qfloat

Коэффициент качества. Безразмерный параметр, характеризующий полосу пропускания -3 дБ режекторного фильтра bw относительно её центральной частоты, Q = w0/bw.

ftype{'notch', 'peak'}

Тип гребенчатого фильтра, генерируемого функцией. Если 'notch', то фактор Q применяется к провалам. Если 'peak', то фактор Q применяется к пикам. По умолчанию 'notch'.

fsfloat, опционально

Частота дискретизации сигнала. По умолчанию 2.0.

pass_zerobool, необязательно

Если False (по умолчанию), провалы (нули) фильтра центрированы на частотах [0, w0, 2*w0, …], а пики центрированы на серединах [w0/2, 3*w0/2, 5*w0/2, …]. Если True, пики центрированы на [0, w0, 2*w0, …] (проходя нулевую частоту) и наоборот.

Добавлено в версии 1.9.0.

Возвращает:

b, aСоздать LinearOperators

Числитель (b) и знаменатель (a) полиномы фильтра IIR.

Вызывает:

ValueError

Если w0 меньше или равна 0 или больше или равна fs/2, если fs не делится на w0, если ftype не является 'notch' или 'peak'

Смотрите также

iirnotch

iirpeak

Примечания

Подробности реализации см. в [1]. Реализация TF гребенчатого фильтра численно устойчива даже при более высоких порядках благодаря использованию одного повторяющегося полюса, который не страдает от потери точности.

Ссылки

[1]

Sophocles J. Orfanidis, «Introduction To Signal Processing», Prentice-Hall, 1996, гл. 11, «Digital Filter Design»

Примеры

Попробуйте в вашем браузере!

Спроектировать и построить гребенчатый фильтр с вырезкой на 20 Гц для сигнала, дискретизированного с частотой 200 Гц, используя добротность Q = 30

>>> from scipy import signal
>>> import matplotlib.pyplot as plt
>>> import numpy as np

>>> fs = 200.0  # Sample frequency (Hz)
>>> f0 = 20.0  # Frequency to be removed from signal (Hz)
>>> Q = 30.0  # Quality factor
>>> # Design notching comb filter
>>> b, a = signal.iircomb(f0, Q, ftype='notch', fs=fs)

>>> # Frequency response
>>> freq, h = signal.freqz(b, a, fs=fs)
>>> response = abs(h)
>>> # To avoid divide by zero when graphing
>>> response[response == 0] = 1e-20
>>> # Plot
>>> fig, ax = plt.subplots(2, 1, figsize=(8, 6), sharex=True)
>>> ax[0].plot(freq, 20*np.log10(abs(response)), color='blue')
>>> ax[0].set_title("Frequency Response")
>>> ax[0].set_ylabel("Amplitude [dB]", color='blue')
>>> ax[0].set_xlim([0, 100])
>>> ax[0].set_ylim([-30, 10])
>>> ax[0].grid(True)
>>> ax[1].plot(freq, (np.angle(h)*180/np.pi+180)%360 - 180, color='green')
>>> ax[1].set_ylabel("Phase [deg]", color='green')
>>> ax[1].set_xlabel("Frequency [Hz]")
>>> ax[1].set_xlim([0, 100])
>>> ax[1].set_yticks([-90, -60, -30, 0, 30, 60, 90])
>>> ax[1].set_ylim([-90, 90])
>>> ax[1].grid(True)
>>> plt.show()

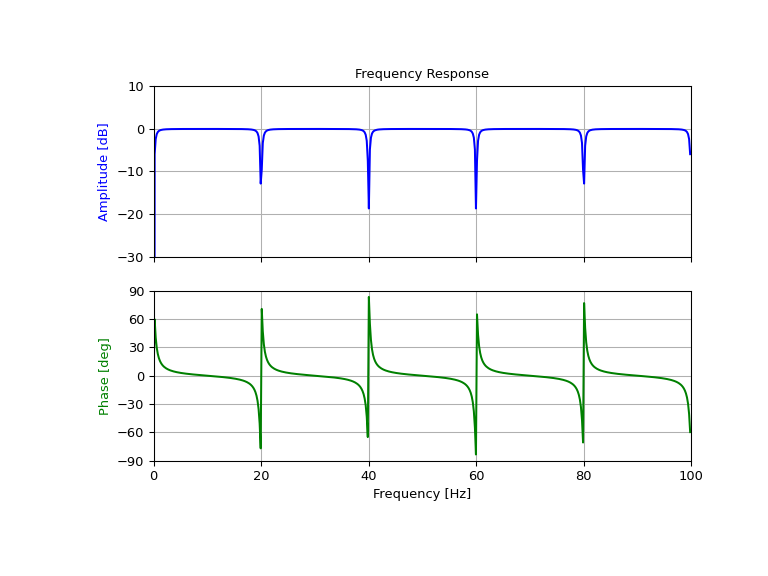
Спроектировать и построить пиковый гребенчатый фильтр на 250 Гц для сигнала, дискретизированного с частотой 1000 Гц, используя добротность Q = 30.

>>> fs = 1000.0  # Sample frequency (Hz)
>>> f0 = 250.0  # Frequency to be retained (Hz)
>>> Q = 30.0  # Quality factor
>>> # Design peaking filter
>>> b, a = signal.iircomb(f0, Q, ftype='peak', fs=fs, pass_zero=True)

>>> # Frequency response
>>> freq, h = signal.freqz(b, a, fs=fs)
>>> response = abs(h)
>>> # To avoid divide by zero when graphing
>>> response[response == 0] = 1e-20
>>> # Plot
>>> fig, ax = plt.subplots(2, 1, figsize=(8, 6), sharex=True)
>>> ax[0].plot(freq, 20*np.log10(np.maximum(abs(h), 1e-5)), color='blue')
>>> ax[0].set_title("Frequency Response")
>>> ax[0].set_ylabel("Amplitude [dB]", color='blue')
>>> ax[0].set_xlim([0, 500])
>>> ax[0].set_ylim([-80, 10])
>>> ax[0].grid(True)
>>> ax[1].plot(freq, (np.angle(h)*180/np.pi+180)%360 - 180, color='green')
>>> ax[1].set_ylabel("Phase [deg]", color='green')
>>> ax[1].set_xlabel("Frequency [Hz]")
>>> ax[1].set_xlim([0, 500])
>>> ax[1].set_yticks([-90, -60, -30, 0, 30, 60, 90])
>>> ax[1].set_ylim([-90, 90])
>>> ax[1].grid(True)
>>> plt.show()

НазадОткрыть во вкладке