scipy.signal.

kaiserord

scipy.signal.kaiserord(пульсация, ширина)

Определить параметры окна фильтра для метода окна Кайзера.

Параметры, возвращаемые этой функцией, обычно используются для создания фильтра с конечной импульсной характеристикой методом окна, с помощью firwin или firwin2.

Параметры:

пульсацияfloat

Верхняя граница отклонения (в дБ) амплитуды частотной характеристики фильтра от желаемой характеристики (не включая частоты в переходных интервалах). То есть, если w - частота, выраженная как доля частоты Найквиста, A(w) - фактическая частотная характеристика фильтра, а D(w) - желаемая частотная характеристика, требование к проектированию состоит в том, что:

abs(A(w) - D(w))) < 10**(-ripple/20)

для 0 <= w <= 1 и w не в переходном интервале.

ширинаfloat

Ширина переходной области, нормированная так, что 1 соответствует π радиан / отсчет. То есть частота выражается как доля частоты Найквиста.

Возвращает:

numtapsint

Длина окна Кайзера.

betafloat

Параметр бета для окна Кайзера.

Смотрите также

kaiser_beta, kaiser_atten

Примечания

Есть несколько способов получить окно Кайзера:

• signal.windows.kaiser(numtaps, beta, sym=True)

• signal.get_window(beta, numtaps)

• signal.get_window(('kaiser', beta), numtaps)

Используются эмпирические уравнения, обнаруженные Кайзером.

Ссылки

Оппенгейм, Шафер, «Обработка дискретных сигналов», стр.475-476.

Примеры

Попробуйте в вашем браузере!

Мы будем использовать метод окна Кайзера для разработки КИХ-фильтра нижних частот для сигнала, дискретизированного с частотой 1000 Гц.

Мы хотим получить как минимум 65 дБ подавления в полосе задерживания, а в полосе пропускания усиление должно изменяться не более чем на 0.5%.

Нам нужна частота среза 175 Гц с переходом между полосой пропускания и полосой задерживания 24 Гц. То есть в полосе [0, 163] усиление изменяется не более чем на 0,5%, а в полосе [187, 500] сигнал ослабляется не менее чем на 65 дБ.

>>> import numpy as np
>>> from scipy.signal import kaiserord, firwin, freqz
>>> import matplotlib.pyplot as plt
>>> fs = 1000.0
>>> cutoff = 175
>>> width = 24

Метод Кайзера принимает только один параметр для управления пульсациями полосы пропускания и подавлением полосы задерживания, поэтому мы используем более строгий из двух. В данном случае пульсация полосы пропускания составляет 0,005 или 46,02 дБ, поэтому мы будем использовать 65 дБ в качестве параметра проектирования.

Используйте kaiserord для определения длины фильтра и параметра для окна Кайзера.

>>> numtaps, beta = kaiserord(65, width/(0.5*fs))
>>> numtaps
167
>>> beta
6.20426

Используйте firwin для создания FIR-фильтра.

>>> taps = firwin(numtaps, cutoff, window=('kaiser', beta),
...               scale=False, fs=fs)

Вычислите частотную характеристику фильтра. w является массивом частот, и h является соответствующим комплексным массивом частотных откликов.

>>> w, h = freqz(taps, worN=8000)
>>> w *= 0.5*fs/np.pi  # Convert w to Hz.

Вычислить отклонение величины отклика фильтра от идеального фильтра нижних частот. Значения в переходной области устанавливаются в nan, поэтому они не появятся на графике.

>>> ideal = w < cutoff  # The "ideal" frequency response.
>>> deviation = np.abs(np.abs(h) - ideal)
>>> deviation[(w > cutoff - 0.5*width) & (w < cutoff + 0.5*width)] = np.nan

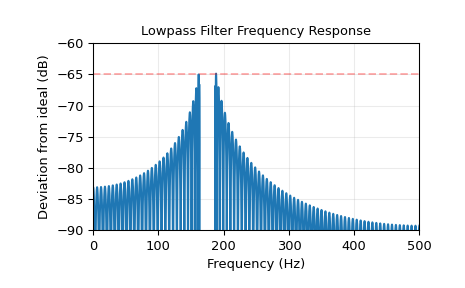
Постройте отклонение. При внимательном рассмотрении левого конца полосы задерживания видно, что требование ослабления на 65 дБ нарушено в первом лепестке примерно на 0.125 дБ. Это не является необычным для метода окна Кайзера.

>>> plt.plot(w, 20*np.log10(np.abs(deviation)))
>>> plt.xlim(0, 0.5*fs)
>>> plt.ylim(-90, -60)
>>> plt.grid(alpha=0.25)
>>> plt.axhline(-65, color='r', ls='--', alpha=0.3)
>>> plt.xlabel('Frequency (Hz)')
>>> plt.ylabel('Deviation from ideal (dB)')
>>> plt.title('Lowpass Filter Frequency Response')
>>> plt.show()

НазадОткрыть во вкладке