scipy.signal.

minimum_phase

scipy.signal.minimum_phase(h, метод='гомоморфный', n_fft=None, *, half=True)

Преобразование линейно-фазового FIR-фильтра в минимально-фазовый

Параметры:

hмассив

Коэффициенты КИХ-фильтра с линейной фазой.

метод{'hilbert', 'homomorphic'}

Предоставленные методы:

‘гомоморфный’ (по умолчанию)

Этот метод [4] [5] лучше всего работает с фильтрами с нечетным числом отводов, и результирующий минимально-фазовый фильтр будет иметь амплитудную характеристику, которая аппроксимирует квадратный корень из амплитудной характеристики исходного фильтра, используя половину числа отводов, когда half=True (по умолчанию), или исходный спектр амплитуд с использованием того же числа отводов, когда half=False.

‘hilbert’

Этот метод [1] предназначен для использования с эквириппильными фильтрами (например, из remez) с областями единичного или нулевого усиления.

n_fftint

Количество точек для использования в БПФ. Должно быть как минимум в несколько раз больше длины сигнала (см. Примечания).

halfbool

Если True, создать фильтр, длина которого вдвое меньше исходного, с амплитудным спектром, являющимся квадратным корнем из исходного. Если False#19864 method='homomorphic').

Добавлено в версии 1.14.0.

Возвращает:

h_minimumмассив

Минимально-фазовая версия фильтра, с длиной (len(h) + 1) // 2 когда half is True или len(h) в противном случае.

Смотрите также

firwin

firwin2

remez

Примечания

Как гильбертово [1] или гомоморфный [4] [5] методы требуют выбора длины БПФ для оценки комплексного кепстра фильтра.

В случае метода Гильберта отклонение от идеального спектра epsilon связано с количеством нулей в полосе задерживания n_stop и длина БПФ n_fft как:

epsilon = 2. * n_stop / n_fft

Например, с 100 нулями в полосе задерживания и длиной БПФ 2048, epsilon = 0.0976. Если мы консервативно предположим, что количество нулей в полосе задерживания на один меньше длины фильтра, мы можем взять длину БПФ как следующую степень двойки, которая удовлетворяет epsilon=0.01 как:

n_fft = 2 ** int(np.ceil(np.log2(2 * (len(h) - 1) / 0.01)))

Это даёт разумные результаты как для метода Гильберта, так и для гомоморфного метода, и даёт значение, используемое при n_fft=None.

Существуют альтернативные реализации для создания минимально-фазовых фильтров, включая инверсию нулей [2] и спектральная факторизация [3] [4]. Для получения дополнительной информации см. эта страница DSPGuru.

Ссылки

[1] (1,2)

N. Damera-Venkata и B. L. Evans, «Оптимальное проектирование вещественных и комплексных минимально-фазовых цифровых КИХ-фильтров», Acoustics, Speech, and Signal Processing, 1999. Proceedings., 1999 IEEE International Conference on, Phoenix, AZ, 1999, pp. 1145-1148 vol.3. DOI:10.1109/ICASSP.1999.756179

[2]

X. Chen и T. W. Parks, "Design of optimal minimum phase FIR filters by direct factorization," Signal Processing, vol. 10, no. 4, pp. 369-383, Jun. 1986.

[3]

Т. Сарамаки, "Проектирование фильтров с конечной импульсной характеристикой," в Справочнике по цифровой обработке сигналов, глава 4, Нью-Йорк: Wiley-Interscience, 1993.

[4] (1,2,3)

J. S. Lim, Advanced Topics in Signal Processing. Englewood Cliffs, N.J.: Prentice Hall, 1988.

[5] (1,2)

A. V. Oppenheim, R. W. Schafer, и J. R. Buck, «Обработка дискретных сигналов», 3-е издание. Upper Saddle River, N.J.: Pearson, 2009.

Примеры

Попробуйте в вашем браузере!

Создать оптимальный линейно-фазовый фильтр нижних частот h с переходной полосой [0.2, 0.3] (предполагая частоту Найквиста 1):

>>> import numpy as np
>>> from scipy.signal import remez, minimum_phase, freqz, group_delay
>>> import matplotlib.pyplot as plt
>>> freq = [0, 0.2, 0.3, 1.0]
>>> desired = [1, 0]
>>> h_linear = remez(151, freq, desired, fs=2)

Преобразовать в минимальную фазу:

>>> h_hil = minimum_phase(h_linear, method='hilbert')
>>> h_hom = minimum_phase(h_linear, method='homomorphic')
>>> h_hom_full = minimum_phase(h_linear, method='homomorphic', half=False)

Сравните импульсную и частотную характеристики четырёх фильтров:

>>> fig0, ax0 = plt.subplots(figsize=(6, 3), tight_layout=True)
>>> fig1, axs = plt.subplots(3, sharex='all', figsize=(6, 6), tight_layout=True)
>>> ax0.set_title("Impulse response")
>>> ax0.set(xlabel='Samples', ylabel='Amplitude', xlim=(0, len(h_linear) - 1))
>>> axs[0].set_title("Frequency Response")
>>> axs[0].set(xlim=(0, .65), ylabel="Magnitude / dB")
>>> axs[1].set(ylabel="Phase / rad")
>>> axs[2].set(ylabel="Group Delay / samples", ylim=(-31, 81),
...             xlabel='Normalized Frequency (Nyqist frequency: 1)')
>>> for h, lb in ((h_linear,   f'Linear ({len(h_linear)})'),
...               (h_hil,      f'Min-Hilbert ({len(h_hil)})'),
...               (h_hom,      f'Min-Homomorphic ({len(h_hom)})'),
...               (h_hom_full, f'Min-Homom. Full ({len(h_hom_full)})')):
...     w_H, H = freqz(h, fs=2)
...     w_gd, gd = group_delay((h, 1), fs=2)
...
...     alpha = 1.0 if lb == 'linear' else 0.5  # full opacity for 'linear' line
...     ax0.plot(h, '.-', alpha=alpha, label=lb)
...     axs[0].plot(w_H, 20 * np.log10(np.abs(H)), alpha=alpha)
...     axs[1].plot(w_H, np.unwrap(np.angle(H)), alpha=alpha, label=lb)
...     axs[2].plot(w_gd, gd, alpha=alpha)
>>> ax0.grid(True)
>>> ax0.legend(title='Filter Phase (Order)')
>>> axs[1].legend(title='Filter Phase (Order)', loc='lower right')
>>> for ax_ in axs:  # shade transition band:
...     ax_.axvspan(freq[1], freq[2], color='y', alpha=.25)
...     ax_.grid(True)
>>> plt.show()

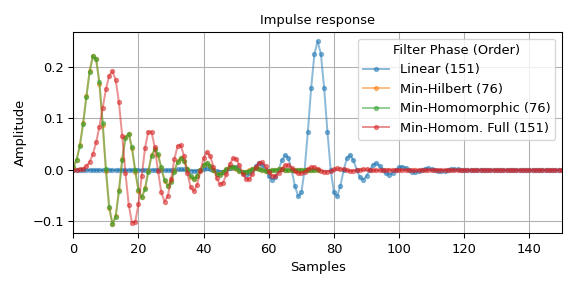
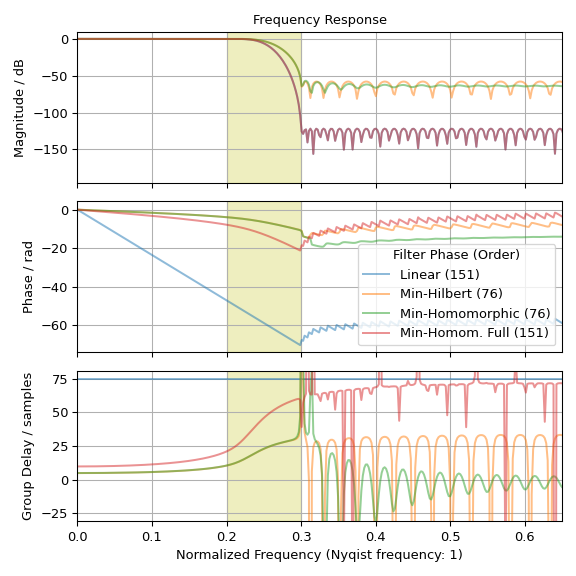
График импульсной характеристики и групповой задержки показывает задержку в 75 выборок для линейного фазового фильтра h. Фаза также должна быть линейной в полосе задерживания — из-за малой величины, числовой шум доминирует там. Кроме того, графики показывают, что фильтры с минимальной фазой явно демонстрируют уменьшенный (отрицательный) наклон фазы в полосе пропускания и переходной полосе. Графики также иллюстрируют, что фильтр с параметрами method='homomorphic', half=False имеет тот же порядок и амплитудную характеристику, что и линейный фильтр h тогда как другие минимально-фазовые фильтры имеют только половину порядка и квадратный корень из амплитудной характеристики.

НазадОткрыть во вкладке