scipy.signal.

lsim#

scipy.signal.lsim(система, U, T, X0=None, interp=True)[источник]#

Моделирование выхода непрерывной линейной системы.

Параметры:
системаэкземпляр класса LTI или кортеж, описывающий систему.

Следующее дает количество элементов в кортеже и их интерпретацию:

  • 1: (экземпляр lti)

  • 2: (num, den)

  • 3: (нули, полюсы, коэффициент усиления)

  • 4: (A, B, C, D)

Uarray_like

Входной массив, описывающий вход на каждом временном шаге T (предполагается интерполяция между заданными временами). Если есть несколько входов, то каждый столбец массива ранга 2 представляет вход. Если U = 0 или None, используется нулевой вход.

Tarray_like

Временные шаги, на которых определён вход и на которых требуется выход. Должны быть неотрицательными, возрастающими и равноотстоящими.

X0array_like, необязательный

Начальные условия для вектора состояния (по умолчанию нулевые).

interpbool, необязательно

Использовать линейную (True, по умолчанию) или интерполяцию нулевого порядка (False) для входного массива.

Возвращает:
T1D ndarray

Временные значения для вывода.

yout1D ndarray

Отклик системы.

xoutndarray

Эволюция вектора состояния во времени.

Примечания

Если (num, den) передано для system, коэффициенты как для числителя, так и для знаменателя должны быть указаны в порядке убывания степени (например, s^2 + 3s + 5 будет представлен как [1, 3, 5]).

Примеры

Мы будем использовать lsim для моделирования аналогового фильтра Бесселя, примененного к сигналу.

>>> import numpy as np
>>> from scipy.signal import bessel, lsim
>>> import matplotlib.pyplot as plt

Создайте фильтр Бесселя нижних частот с частотой среза 12 Гц.

>>> b, a = bessel(N=5, Wn=2*np.pi*12, btype='lowpass', analog=True)

Сгенерировать данные, к которым применяется фильтр.

>>> t = np.linspace(0, 1.25, 500, endpoint=False)

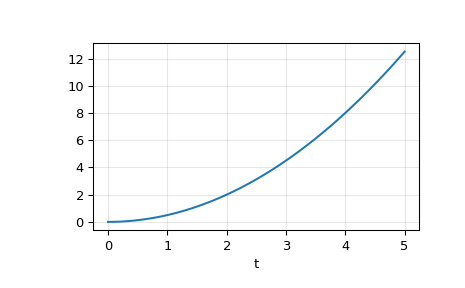
Входной сигнал - сумма трех синусоидальных кривых с частотами 4 Гц, 40 Гц и 80 Гц. Фильтр должен в основном устранять компоненты 40 Гц и 80 Гц, оставляя только сигнал 4 Гц.

>>> u = (np.cos(2*np.pi*4*t) + 0.6*np.sin(2*np.pi*40*t) +
...      0.5*np.cos(2*np.pi*80*t))

Смоделировать фильтр с lsim.

>>> tout, yout, xout = lsim((b, a), U=u, T=t)

Построить результат.

>>> plt.plot(t, u, 'r', alpha=0.5, linewidth=1, label='input')
>>> plt.plot(tout, yout, 'k', linewidth=1.5, label='output')
>>> plt.legend(loc='best', shadow=True, framealpha=1)
>>> plt.grid(alpha=0.3)
>>> plt.xlabel('t')
>>> plt.show()
../../_images/scipy-signal-lsim-1_00_00.png

Во втором примере мы моделируем двойной интегратор y'' = u, с постоянным входом u = 1. Мы будем использовать представление пространства состояний интегратора.

>>> from scipy.signal import lti
>>> A = np.array([[0.0, 1.0], [0.0, 0.0]])
>>> B = np.array([[0.0], [1.0]])
>>> C = np.array([[1.0, 0.0]])
>>> D = 0.0
>>> system = lti(A, B, C, D)

t и u определить время и входной сигнал для моделируемой системы.

>>> t = np.linspace(0, 5, num=50)
>>> u = np.ones_like(t)

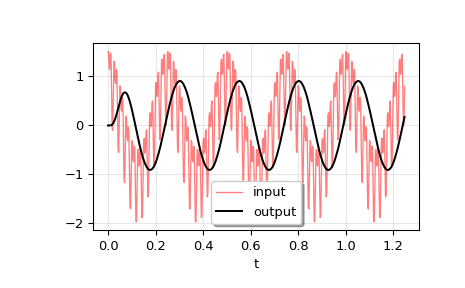
Выполнить моделирование, а затем построить график y. Как и ожидалось, график показывает кривую y = 0.5*t**2.

>>> tout, y, x = lsim(system, u, t)
>>> plt.plot(t, y)
>>> plt.grid(alpha=0.3)
>>> plt.xlabel('t')
>>> plt.show()
../../_images/scipy-signal-lsim-1_01_00.png
На этой странице