sweep_poly#
- scipy.signal.sweep_poly(t, poly, phi=0)[источник]#
Генератор косинуса с изменяющейся частотой, зависящей от времени.
Эта функция генерирует синусоидальную функцию, мгновенная частота которой изменяется со временем. Частота в момент времени t задаётся полиномом poly.
- Параметры:
- tndarray
Временные точки для вычисления формы сигнала.
- poly1-D array_like или экземпляр numpy.poly1d
Желаемая частота, выраженная в виде полинома. Если poly является списком или ndarray длины n, то элементы poly являются коэффициентами полинома, а мгновенная частота
f(t) = poly[0]*t**(n-1) + poly[1]*t**(n-2) + ... + poly[n-1]Если poly является экземпляром numpy.poly1d, тогда мгновенная частота равна
f(t) = poly(t)- phifloat, опционально
Фазовый сдвиг, в градусах, по умолчанию: 0.
- Возвращает:
- sweep_polyndarray
Массив numpy, содержащий сигнал, вычисленный в t с запрошенной изменяющейся во времени частотой. Более точно, функция возвращает
cos(phase + (pi/180)*phi), где фаза является интегралом (от 0 до t) от2 * pi * f(t);f(t)определено выше.
Смотрите также
Примечания
Добавлено в версии 0.8.0.
Если poly является списком или ndarray длины n, тогда элементы poly являются коэффициентами полинома, а мгновенная частота равна:
f(t) = poly[0]*t**(n-1) + poly[1]*t**(n-2) + ... + poly[n-1]Если poly является экземпляром
numpy.poly1d, тогда мгновенная частота равна:f(t) = poly(t)Наконец, выходные данные s равен:
cos(phase + (pi/180)*phi)где фаза является интегралом от 0 до t of
2 * pi * f(t),f(t)как определено выше.Примеры
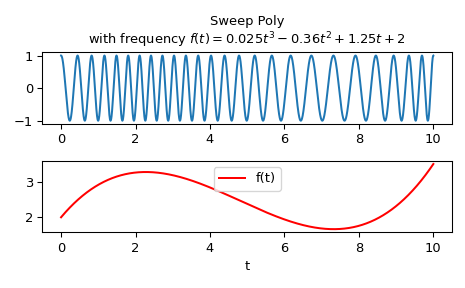
Вычислить форму сигнала с мгновенной частотой:
f(t) = 0.025*t**3 - 0.36*t**2 + 1.25*t + 2
на интервале 0 <= t <= 10.
>>> import numpy as np >>> from scipy.signal import sweep_poly >>> p = np.poly1d([0.025, -0.36, 1.25, 2.0]) >>> t = np.linspace(0, 10, 5001) >>> w = sweep_poly(t, p)
Построить график:
>>> import matplotlib.pyplot as plt >>> plt.subplot(2, 1, 1) >>> plt.plot(t, w) >>> plt.title("Sweep Poly\nwith frequency " + ... "$f(t) = 0.025t^3 - 0.36t^2 + 1.25t + 2$") >>> plt.subplot(2, 1, 2) >>> plt.plot(t, p(t), 'r', label='f(t)') >>> plt.legend() >>> plt.xlabel('t') >>> plt.tight_layout() >>> plt.show()