scipy.signal.

чирп

scipy.signal.чирп(t, f0, t1, f1, метод='linear', phi=0, vertex_zero=True, *, комплексный=False)

Генератор косинуса с изменяющейся частотой.

В дальнейшем 'Гц' следует интерпретировать как 'циклов на единицу'; здесь не требуется, чтобы единица была одной секундой. Важное различие заключается в том, что единицы вращения - это циклы, а не радианы. Аналогично, t может быть измерением пространства вместо времени.

Параметры:

tarray_like

Временные точки для вычисления формы сигнала.

f0float

Частота (например, Гц) в момент времени t=0.

t1float

Время, в которое f1 указан.

f1float

Частота (например, Гц) формы сигнала во время t1.

метод{‘linear’, ‘quadratic’, ‘logarithmic’, ‘hyperbolic’}, опционально

Тип частотной развёртки. Если не задан, линейный предполагается. См. Примечания ниже для более подробной информации.

phifloat, опционально

Фазовый сдвиг, в градусах. По умолчанию 0.

vertex_zerobool, необязательно

Этот параметр используется только когда метод равно 'quadratic'. Он определяет, находится ли вершина параболы, которая является графиком частоты, в t=0 или t=t1.

комплексныйbool, необязательно

Этот параметр создает комплексный аналитический сигнал вместо вещественного. Он позволяет использовать комплексную полосу (в области связи). По умолчанию False.

Добавлено в версии 1.15.0.

Возвращает:

yndarray

Массив numpy, содержащий сигнал, вычисленный в t с запрошенной частотой, изменяющейся во времени. Более точно, функция возвращает exp(1j*phase + 1j*(pi/180)*phi) if complex else cos(phase + (pi/180)*phi) где фаза это интеграл (от 0 до t) из 2*pi*f(t). Мгновенная частота f(t) определен ниже.

Смотрите также

sweep_poly

Примечания

Существует четыре возможных варианта для параметра метод, которые имеют (длинную) стандартную форму и некоторые допустимые сокращения. Формулы для мгновенной частоты \(f(t)\) сгенерированного сигнала следующие:

1. Параметр метод в ('linear', 'lin', 'li'):

   \[f(t) = f_0 + \beta\, t \quad\text{with}\quad \beta = \frac{f_1 - f_0}{t_1}\]

   Частота \(f(t)\) изменяется линейно во времени с постоянной скоростью \(\beta\).

2. Параметр метод в ('quadratic', 'quad', 'q'):

   \[\begin{split}f(t) = \begin{cases} f_0 + \beta\, t^2 & \text{if vertex_zero is True,}\\ f_1 + \beta\, (t_1 - t)^2 & \text{otherwise,} \end{cases} \quad\text{with}\quad \beta = \frac{f_1 - f_0}{t_1^2}\end{split}\]

   График частоты f(t) является параболой через \((0, f_0)\) и \((t_1, f_1)\). По умолчанию вершина параболы находится в \((0, f_0)\). Если vertex_zero является False, тогда вершина находится в \((t_1, f_1)\). Чтобы использовать более общую квадратичную функцию или произвольный полином, используйте функцию scipy.signal.sweep_poly.

3. Параметр метод в ('logarithmic', 'log', 'lo'):

   \[f(t) = f_0 \left(\frac{f_1}{f_0}\right)^{t/t_1}\]

   \(f_0\) и \(f_1\) должно быть ненулевым и иметь одинаковый знак. Этот сигнал также известен как геометрический или экспоненциальный чирп.

4. Параметр метод в ('hyperbolic', 'hyp'):

   \[f(t) = \frac{\alpha}{\beta\, t + \gamma} \quad\text{with}\quad \alpha = f_0 f_1 t_1, \ \beta = f_0 - f_1, \ \gamma = f_1 t_1\]

   \(f_0\) и \(f_1\) должно быть ненулевым.

Примеры

Попробуйте в вашем браузере!

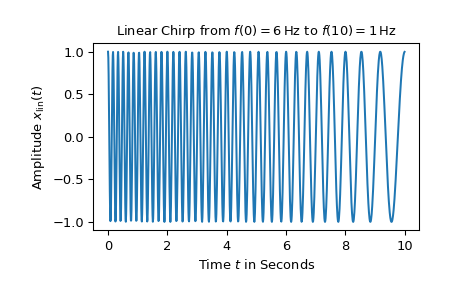
Для первого примера линейный чирп в диапазоне от 6 Гц до 1 Гц за 10 секунд отображается:

>>> import numpy as np
>>> from matplotlib.pyplot import tight_layout
>>> from scipy.signal import chirp, square, ShortTimeFFT
>>> from scipy.signal.windows import gaussian
>>> import matplotlib.pyplot as plt
...
>>> N, T = 1000, 0.01  # number of samples and sampling interval for 10 s signal
>>> t = np.arange(N) * T  # timestamps
...
>>> x_lin = chirp(t, f0=6, f1=1, t1=10, method='linear')
...
>>> fg0, ax0 = plt.subplots()
>>> ax0.set_title(r"Linear Chirp from $f(0)=6\,$Hz to $f(10)=1\,$Hz")
>>> ax0.set(xlabel="Time $t$ in Seconds", ylabel=r"Amplitude $x_\text{lin}(t)$")
>>> ax0.plot(t, x_lin)
>>> plt.show()

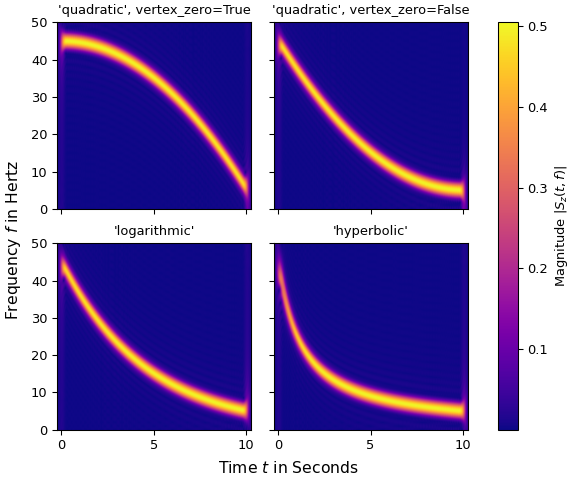
На следующих четырёх графиках показано кратковременное преобразование Фурье чирпа, изменяющегося от 45 Гц до 5 Гц с различными значениями параметра метод (и vertex_zero):

>>> x_qu0 = chirp(t, f0=45, f1=5, t1=N*T, method='quadratic', vertex_zero=True)
>>> x_qu1 = chirp(t, f0=45, f1=5, t1=N*T, method='quadratic', vertex_zero=False)
>>> x_log = chirp(t, f0=45, f1=5, t1=N*T, method='logarithmic')
>>> x_hyp = chirp(t, f0=45, f1=5, t1=N*T, method='hyperbolic')
...
>>> win = gaussian(50, std=12, sym=True)
>>> SFT = ShortTimeFFT(win, hop=2, fs=1/T, mfft=800, scale_to='magnitude')
>>> ts = ("'quadratic', vertex_zero=True", "'quadratic', vertex_zero=False",
...       "'logarithmic'", "'hyperbolic'")
>>> fg1, ax1s = plt.subplots(2, 2, sharex='all', sharey='all',
...                          figsize=(6, 5),  layout="constrained")
>>> for x_, ax_, t_ in zip([x_qu0, x_qu1, x_log, x_hyp], ax1s.ravel(), ts):
...     aSx = abs(SFT.stft(x_))
...     im_ = ax_.imshow(aSx, origin='lower', aspect='auto', extent=SFT.extent(N),
...                      cmap='plasma')
...     ax_.set_title(t_)
...     if t_ == "'hyperbolic'":
...         fg1.colorbar(im_, ax=ax1s, label='Magnitude $|S_z(t,f)|$')
>>> _ = fg1.supxlabel("Time $t$ in Seconds")  # `_ =` is needed to pass doctests
>>> _ = fg1.supylabel("Frequency $f$ in Hertz")
>>> plt.show()

Наконец, кратковременное преобразование Фурье комплекснозначного линейного чирпа в диапазоне от -30 Гц до 30 Гц изображено:

>>> z_lin = chirp(t, f0=-30, f1=30, t1=N*T, method="linear", complex=True)
>>> SFT.fft_mode = 'centered'  # needed to work with complex signals
>>> aSz = abs(SFT.stft(z_lin))
...
>>> fg2, ax2 = plt.subplots()
>>> ax2.set_title(r"Linear Chirp from $-30\,$Hz to $30\,$Hz")
>>> ax2.set(xlabel="Time $t$ in Seconds", ylabel="Frequency $f$ in Hertz")
>>> im2 = ax2.imshow(aSz, origin='lower', aspect='auto',
...                  extent=SFT.extent(N), cmap='viridis')
>>> fg2.colorbar(im2, label='Magnitude $|S_z(t,f)|$')
>>> plt.show()

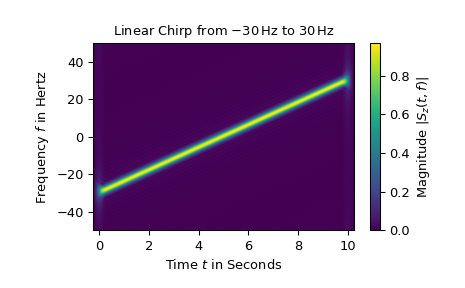
Обратите внимание, что использование отрицательных частот имеет смысл только для комплекснозначных сигналов. Кроме того, модуль комплексной экспоненциальной функции равен единице, тогда как модуль вещественной косинусной функции составляет только 1/2.

НазадОткрыть во вкладке