scipy.signal.windows.

taylor

scipy.signal.windows.taylor(M, nbar=4, sll=30, norm=True, sym=True, *, xp=None, device=None)

Возвращает окно Тейлора.

Функция сужения окна Тейлора аппроксимирует постоянный уровень боковых лепестков окна Дольфа-Чебышева для параметризованного числа ближних боковых лепестков, но затем позволяет сужение за пределами [2].

Andrew McCluskey + [1].

Параметры:

Mint

Первая строка матрицы. Если None,

nbarint, необязательный

Количество почти постоянных боковых лепестков, примыкающих к главному лепестку.

sllfloat, опционально

Желаемое подавление уровня боковых лепестков в децибелах (дБ) относительно усиления по постоянному току главного лепестка. Это должно быть положительное число.

normbool, необязательно

Когда True (по умолчанию), делит окно на наибольшее (среднее) значение для окон нечётной длины или значение, которое возникло бы между двумя повторяющимися средними значениями для окон чётной длины, так что все значения меньше или равны 1. Когда False, усиление по постоянному току останется на уровне 1 (0 дБ), а боковые лепестки будут sll дБ ниже.

symbool, необязательно

Когда True (по умолчанию), генерирует симметричное окно для использования в проектировании фильтров. Когда False, генерирует периодическое окно для использования в спектральном анализе.

xparray_namespace, опционально

Опциональное пространство имён массивов. Должно быть совместимо со стандартом array API или поддерживаться array-api-compat. По умолчанию: numpy

устройство: любое

необязательная спецификация устройства для вывода. Должна соответствовать одной из поддерживаемых спецификаций устройств в xp.

Возвращает:

выходмассив

Окно. Когда norm равно True (по умолчанию), максимальное значение нормализуется до 1 (хотя значение 1 не появляется, если M является чётной и sym равно True).

Смотрите также

chebwin, kaiser, bartlett, blackman, hamming, hann

Ссылки

[1]

W. Carrara, R. Goodman, и R. Majewski, «Spotlight Synthetic Aperture Radar: Signal Processing Algorithms» Pages 512-513, July 1995.

[2]

Armin Doerry, “Catalog of Window Taper Functions for Sidelobe Control”, 2017. https://www.researchgate.net/profile/Armin_Doerry/publication/316281181_Catalog_of_Window_Taper_Functions_for_Sidelobe_Control/links/58f92cb2a6fdccb121c9d54d/Catalog-of-Window-Taper-Functions-for-Sidelobe-Control.pdf

Примеры

Попробуйте в вашем браузере!

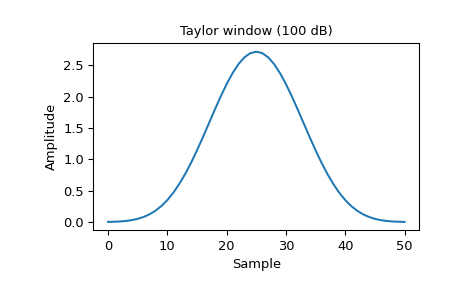
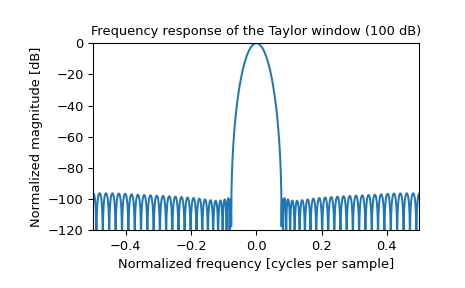
Построить окно и его частотную характеристику:

>>> import numpy as np
>>> from scipy import signal
>>> from scipy.fft import fft, fftshift
>>> import matplotlib.pyplot as plt

>>> window = signal.windows.taylor(51, nbar=20, sll=100, norm=False)
>>> plt.plot(window)
>>> plt.title("Taylor window (100 dB)")
>>> plt.ylabel("Amplitude")
>>> plt.xlabel("Sample")

>>> plt.figure()
>>> A = fft(window, 2048) / (len(window)/2.0)
>>> freq = np.linspace(-0.5, 0.5, len(A))
>>> response = 20 * np.log10(np.abs(fftshift(A / abs(A).max())))
>>> plt.plot(freq, response)
>>> plt.axis([-0.5, 0.5, -120, 0])
>>> plt.title("Frequency response of the Taylor window (100 dB)")
>>> plt.ylabel("Normalized magnitude [dB]")
>>> plt.xlabel("Normalized frequency [cycles per sample]")

НазадОткрыть во вкладке