scipy.spatial.

Delaunay

класс scipy.spatial.Delaunay(точки, furthest_site=False, инкрементальных=False, qhull_options=None)

Триангуляция Делоне в N измерениях.

Добавлено в версии 0.9.

Параметры:

точкиndarray из float, форма (npoints, ndim)

Координаты точек для триангуляции

furthest_sitebool, необязательно

Вычислять ли триангуляцию Делоне для наиболее удаленных точек. По умолчанию: False

Добавлено в версии 0.12.0.

инкрементальныхbool, необязательно

Разрешить добавление новых точек инкрементально. Это требует некоторых дополнительных ресурсов.

qhull_optionsstr, optional

Дополнительные опции для передачи в Qhull. Подробности см. в руководстве Qhull. Опция "Qt" всегда включена. По умолчанию: "Qbb Qc Qz Qx Q12" для ndim > 4 и "Qbb Qc Qz Q12" в остальных случаях. В инкрементальном режиме пропускается "Qz".

Добавлено в версии 0.12.0.

Атрибуты:

точкиndarray типа double, форма (npoints, ndim)

Координаты входных точек.

симплексыndarray целых чисел, форма (nsimplex, ndim+1)

Индексы точек, образующих симплексы в триангуляции. Для 2-D точки ориентированы против часовой стрелки.

соседиndarray целых чисел, форма (nsimplex, ndim+1)

Индексы соседних симплексов для каждого симплекса. K-й сосед противоположен k-й вершине. Для симплексов на границе -1 означает отсутствие соседа.

уравненияndarray типа double, форма (nsimplex, ndim+2)

[normal, offset], формирующие уравнение гиперплоскости грани на параболоиде (см. Документация Qhull для получения дополнительной информации).

paraboloid_scale, paraboloid_shiftfloat

Масштаб и сдвиг для дополнительного параболоидного измерения (см. Документация Qhull для получения дополнительной информации).

transformndarray типа double, форма (nsimplex, ndim+1, ndim)

Аффинное преобразование из x к барицентрическим координатам c.

vertex_to_simplexndarray of int, shape (npoints,)

Массив поиска, от вершины к некоторому симплексу, частью которого она является.

convex_hullndarray из int, форма (nfaces, ndim)

Вершины граней, образующих выпуклую оболочку набора точек.

компланарныйndarray из int, форма (ncoplanar, 3)

Индексы компланарных точек и соответствующие индексы ближайшей грани и ближайшей вершины. Компланарные точки - это входные точки, которые были не включен в триангуляцию из-за проблем с численной точностью.

Если опция "Qc" не указана, этот список не вычисляется.

Добавлено в версии 0.12.0.

vertex_neighbor_verticesкортеж из двух ndarrays int; (indptr, indices)

Соседние вершины вершин.

furthest_site

True, если это была триангуляция по наиболее удалённым точкам, и False, если нет.

Добавлено в версии 1.4.0.

Методы

add_points(points[, restart])	Обработать набор дополнительных новых точек.
close()	Завершить инкрементную обработку.
find_simplex(self, xi[, bruteforce, tol])	Найти симплексы, содержащие заданные точки.
lift_points(self, x)	Поднимите точки до параболоида Qhull.
plane_distance(self, xi)	Вычислить расстояния от точки до гиперплоскостей xi из всех симплексов.

Вызывает:

QhullError

Возникает, когда Qhull сталкивается с ошибкой, например, геометрической вырожденностью, когда опции для разрешения не включены.

ValueError

Возникает, если на вход подается несовместимый массив.

Примечания

Тесселяция вычисляется с использованием библиотеки Qhull Библиотека Qhull.

Примечание

Если вы не передаёте опцию Qhull "QJ", Qhull не гарантирует, что каждая входная точка будет вершиной в триангуляции Делоне. Пропущенные точки перечислены в компланарный атрибут.

Примеры

Попробуйте в вашем браузере!

Триангуляция набора точек:

>>> import numpy as np
>>> points = np.array([[0, 0], [0, 1.1], [1, 0], [1, 1]])
>>> from scipy.spatial import Delaunay
>>> tri = Delaunay(points)

Мы можем построить график:

>>> import matplotlib.pyplot as plt
>>> plt.triplot(points[:,0], points[:,1], tri.simplices)
>>> plt.plot(points[:,0], points[:,1], 'o')
>>> plt.show()

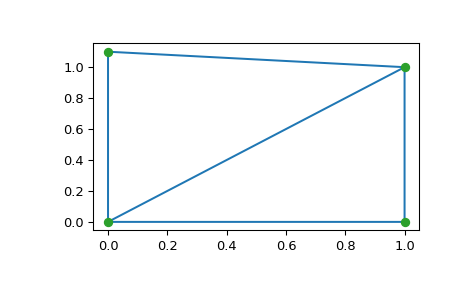
Индексы точек и координаты для двух треугольников, образующих триангуляцию:

>>> tri.simplices
array([[2, 3, 0],                 # may vary
       [3, 1, 0]], dtype=int32)

Обратите внимание, что в зависимости от того, как идут ошибки округления, симплексы могут быть в другом порядке, чем выше.

>>> points[tri.simplices]
array([[[ 1. ,  0. ],            # may vary
        [ 1. ,  1. ],
        [ 0. ,  0. ]],
       [[ 1. ,  1. ],
        [ 0. ,  1.1],
        [ 0. ,  0. ]]])

Треугольник 0 является единственным соседом треугольника 1, и он противоположен вершине 1 треугольника 1:

>>> tri.neighbors[1]
array([-1,  0, -1], dtype=int32)
>>> points[tri.simplices[1,1]]
array([ 0. ,  1.1])

Мы можем определить, в каком треугольнике находятся точки:

>>> p = np.array([(0.1, 0.2), (1.5, 0.5), (0.5, 1.05)])
>>> tri.find_simplex(p)
array([ 1, -1, 1], dtype=int32)

Возвращаемые целые числа в массиве — это индексы симплекса, в котором находится соответствующая точка. Если возвращается -1, точка не находится ни в одном симплексе. Учтите, что сокращение в следующем примере работает корректно только для валидных точек, так как невалидные точки дают -1, который сам является валидным индексом для последнего симплекса в списке.

>>> p_valids = np.array([(0.1, 0.2), (0.5, 1.05)])
>>> tri.simplices[tri.find_simplex(p_valids)]
array([[3, 1, 0],                 # may vary
       [3, 1, 0]], dtype=int32)

Мы также можем вычислить барицентрические координаты в треугольнике 1 для этих точек:

>>> b = tri.transform[1,:2].dot(np.transpose(p - tri.transform[1,2]))
>>> np.c_[np.transpose(b), 1 - b.sum(axis=0)]
array([[ 0.1       ,  0.09090909,  0.80909091],
       [ 1.5       , -0.90909091,  0.40909091],
       [ 0.5       ,  0.5       ,  0.        ]])

Координаты первой точки все положительны, что означает, что она действительно внутри треугольника. Третья точка находится на ребре, отсюда ее нулевая третья координата.

НазадОткрыть во вкладке