scipy.spatial.transform.

RigidTransform

класс scipy.spatial.transform.RigidTransform

Жесткое преобразование в 3-х измерениях.

Этот класс предоставляет интерфейс для инициализации и представления жёстких преобразований (вращение и перенос) в 3D-пространстве. В разных областях этот тип преобразования может называться «pose” (особенно в робототехнике), “внешние параметры”, или “матрица модели” (особенно в компьютерной графике), но основная концепция та же: вращение и перемещение, описывающие ориентацию одной 3D системы координат относительно другой. Математически эти преобразования принадлежат специальной евклидовой группе SE(3), которая кодирует вращение (SO(3)) плюс перемещение.

Поддерживаются следующие операции над жёсткими преобразованиями:

• Применение к векторам

• Композиция преобразований

• Инверсия преобразования

• Индексация преобразования

Обратите внимание, что системы координат должны быть правыми. Из-за этого этот класс более точно представляет правильный жесткие преобразования в SE(3) вместо жестких преобразований в E(3) в более общем случае [1].

Индексирование внутри преобразования поддерживается, так как несколько преобразований могут быть сохранены в одном RigidTransform экземпляр.

Чтобы создать RigidTransform объекты используют from_... методы (см. примеры ниже). RigidTransform(...) не предназначен для непосредственного создания экземпляра.

Для строгих введений в жесткие преобразования, см. [2], [3], и [4].

Атрибуты:

single

Представляет ли этот экземпляр одно преобразование.

rotation

Вернуть компонент вращения преобразования.

translation

Возвращает компонент трансляции преобразования.

Методы

__len__(self)	Возвращает количество преобразований в этом объекте.
__getitem__(self, indexer)	Извлечь преобразование(я) по заданным индексам из этого объекта.
__mul__(self, RigidTransform other)	Скомбинировать это преобразование с другим.
__pow__(self, float n)	Композиция этого преобразования с самим собой n раз.
from_matrix(cls, matrix)	Инициализировать из матрицы преобразования 4x4.
from_rotation(cls, rotation)	Инициализировать из вращения, без перемещения.
from_translation(cls, translation)	Инициализация из массива numpy сдвига, без вращения.
from_components(cls, translation, rotation)	Инициализация жесткого преобразования из компонентов трансляции и вращения.
from_exp_coords(cls, exp_coords)	Инициализация из экспоненциальных координат преобразования.
from_dual_quat(cls, dual_quat, *[, scalar_first])	Инициализация из единичного двойного кватерниона.
as_matrix(self)	Вернуть копию матричного представления преобразования.
as_components(self)	Возвращает компоненты трансляции и вращения преобразования, где вращение применяется первым, за которым следует трансляция.
as_exp_coords(self)	Возвращает экспоненциальные координаты преобразования.
as_dual_quat(self, *[, scalar_first])	Возвращает представление преобразования в виде двойного кватерниона.
concatenate(cls, transforms)	Объединить последовательность RigidTransform объектов в единый объект.
apply(self, vector[, inverse])	Применить преобразование к вектору.
inv(self)	Инвертировать это преобразование.
identity(cls[, num])	Инициализировать тождественное преобразование.

Примечания

Добавлено в версии 1.16.0.

Ссылки

[1]

https://en.wikipedia.org/wiki/Rigid_transformation

[2]

https://motion.cs.illinois.edu/RoboticSystems/CoordinateTransformations.html

[3]

https://www.brainvoyager.com/bv/doc/UsersGuide/CoordsAndTransforms/SpatialTransformationMatrices.html

[4]

Kevin M. Lynch и Frank C. Park, "Modern Robotics: Mechanics, Planning, and Control" Глава 3.3, 2017, Cambridge University Press. https://hades.mech.northwestern.edu/images/2/25/MR-v2.pdf#page=107.31

[5]

Пол Фергейл, «Представление позы робота: хорошее, плохое и ужасное», 9 июня 2014 г. https://rpg.ifi.uzh.ch/docs/teaching/2024/FurgaleTutorial.pdf

Примеры

Попробуйте в вашем браузере!

A RigidTransform экземпляр может быть инициализирован в любом из вышеуказанных форматов и преобразован в любой другой. Базовый объект не зависит от представления, используемого для инициализации.

Соглашения об обозначениях и композиция

Обозначения здесь в основном следуют соглашению, определённому в [5]. Когда мы называем преобразования, мы читаем индексы справа налево. Таким образом, tf_A_B представляет преобразование A <- B и может интерпретироваться как:

• координатах и ориентации B относительно A

• преобразование точек из B в A

• положение B, описанное в системе координат A

tf_A_B
   ^ ^
   | |
   | --- from B
   |
   ----- to A

При композиции преобразований важен порядок. Преобразования не коммутативны, поэтому в общем случае tf_A_B * tf_B_C не то же самое, что tf_B_C * tf_A_B. Преобразования компонуются и применяются к векторам справа налево. Таким образом, (tf_A_B * tf_B_C).apply(p_C) то же самое, что tf_A_B.apply(tf_B_C.apply(p_C)).

При композиции преобразования должны быть упорядочены так, чтобы оператор умножения был окружён одним кадром, чтобы кадр «сокращался» и оставались внешние кадры. В примере ниже B сокращается, и остаются внешние кадры A и C. Или, другими словами, A <- C — это то же самое, что A <- B <- C.

              ----------- B cancels out
              |      |
              v      v
tf_A_C = tf_A_B * tf_B_C
            ^          ^
            |          |
            ------------ to A, from C are left

При обозначении векторов мы пишем индекс системы отсчёта, в которой определён вектор. Таким образом, p_B означает точку p определённый в системе координат B. Чтобы преобразовать эту точку из системы координат B в координаты системы A, мы применяем преобразование tf_A_B к вектору, выравнивая элементы так, чтобы обозначенные B-кадры находились рядом и "сокращались".

           ------------ B cancels out
           |         |
           v         v
p_A = tf_A_B.apply(p_B)
         ^
         |
         -------------- A is left

Визуализация

>>> from scipy.spatial.transform import RigidTransform as Tf
>>> from scipy.spatial.transform import Rotation as R
>>> import numpy as np

Следующая функция может использоваться для построения преобразований с помощью Matplotlib, показывая, как они преобразуют стандартные оси координат x, y, z:

>>> import matplotlib.pyplot as plt
>>> colors = ("#FF6666", "#005533", "#1199EE")  # Colorblind-safe RGB
>>> def plot_transformed_axes(ax, tf, name=None, scale=1):
...     r = tf.rotation
...     t = tf.translation
...     loc = np.array([t, t])
...     for i, (axis, c) in enumerate(zip((ax.xaxis, ax.yaxis, ax.zaxis),
...                                       colors)):
...         axlabel = axis.axis_name
...         axis.set_label_text(axlabel)
...         axis.label.set_color(c)
...         axis.line.set_color(c)
...         axis.set_tick_params(colors=c)
...         line = np.zeros((2, 3))
...         line[1, i] = scale
...         line_rot = r.apply(line)
...         line_plot = line_rot + loc
...         ax.plot(line_plot[:, 0], line_plot[:, 1], line_plot[:, 2], c)
...         text_loc = line[1]*1.2
...         text_loc_rot = r.apply(text_loc)
...         text_plot = text_loc_rot + t
...         ax.text(*text_plot, axlabel.upper(), color=c,
...                 va="center", ha="center")
...     ax.text(*tf.translation, name, color="k", va="center", ha="center",
...             bbox={"fc": "w", "alpha": 0.8, "boxstyle": "circle"})

Определение систем координат

Давайте рассмотрим пример.

Сначала определите "мировую систему координат" A, также называемую "базовой системой координат". Все системы координат являются тождественным преобразованием с их собственной точки зрения.

>>> tf_A = Tf.identity()

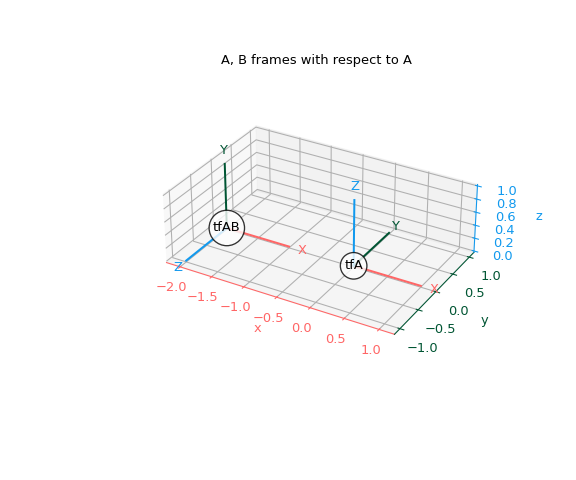
Мы визуализируем новый кадр B в системе координат A. Поэтому нам нужно определить преобразование, которое преобразует координаты из кадра B в кадр A (A <- B).

Физически представим построение B из A следующим образом:

1. Поворот A на +90 градусов вокруг своей оси x.

2. Перемещение повёрнутой системы координат на 2 единицы в направлении -x системы A.

С точки зрения A, B находится в точке [-2, 0, 0] и повёрнут на +90 градусов вокруг оси x, что в точности соответствует преобразованию A <- B.

>>> t_A_B = np.array([-2, 0, 0])
>>> r_A_B = R.from_euler('xyz', [90, 0, 0], degrees=True)
>>> tf_A_B = Tf.from_components(t_A_B, r_A_B)

Давайте построим эти кадры.

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_A, name="tfA")     # A plotted in A
>>> plot_transformed_axes(ax, tf_A_B, name="tfAB")  # B plotted in A
>>> ax.set_title("A, B frames with respect to A")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

Теперь визуализируем новый фрейм C в системе координат B. Представим, что C строится из B путем:

1. Перемещение B на 2 единицы в направлении +z.

2. Поворот B на +30 градусов вокруг его оси z.

>>> t_B_C = np.array([0, 0, 2])
>>> r_B_C = R.from_euler('xyz', [0, 0, 30], degrees=True)
>>> tf_B_C = Tf.from_components(t_B_C, r_B_C)

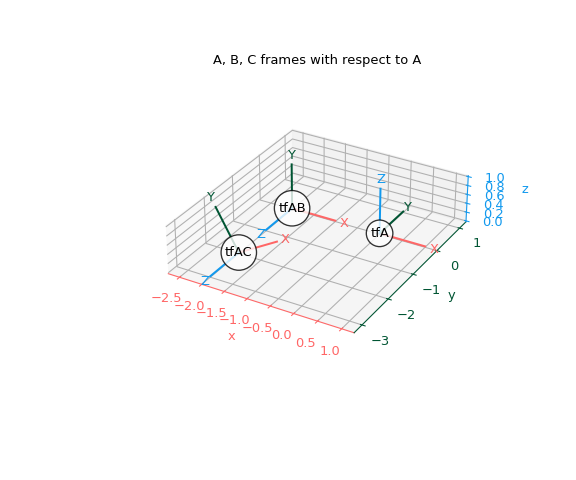
Чтобы построить эти кадры с единой точки зрения, нам нужно вычислить преобразование между A и C. Обратите внимание, что мы не делаем это преобразование напрямую, а вместо этого составляем промежуточные преобразования, которые позволяют нам перейти от C к A:

>>> tf_A_C = tf_A_B * tf_B_C  # A <- B <- C

Теперь мы можем построить эти три кадра с точки зрения A.

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_A, name="tfA")     # A plotted in A
>>> plot_transformed_axes(ax, tf_A_B, name="tfAB")  # B plotted in A
>>> plot_transformed_axes(ax, tf_A_C, name="tfAC")  # C plotted in A
>>> ax.set_title("A, B, C frames with respect to A")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

Преобразование векторов

Давайте преобразуем вектор из A в B и C. Для этого сначала инвертируем преобразования, которые у нас уже есть из B и C в A.

>>> tf_B_A = tf_A_B.inv()  # B <- A
>>> tf_C_A = tf_A_C.inv()  # C <- A

Теперь мы можем определить точку в A и использовать приведенные выше преобразования для получения её координат в B и C:

>>> p1_A = np.array([1, 0, 0])  # +1 in x_A direction
>>> p1_B = tf_B_A.apply(p1_A)
>>> p1_C = tf_C_A.apply(p1_A)
>>> print(p1_A)  # Original point 1 in A
[1 0 0]
>>> print(p1_B)  # Point 1 in B
[3. 0. 0.]
>>> print(p1_C)  # Point 1 in C
[ 2.59807621 -1.5       -2.        ]

Мы также можем сделать обратное. Определяем точку в C и преобразуем её в A:

>>> p2_C = np.array([0, 1, 0])  # +1 in y_C direction
>>> p2_A = tf_A_C.apply(p2_C)
>>> print(p2_C)  # Original point 2 in C
[0 1 0]
>>> print(p2_A)  # Point 2 in A
[-2.5       -2.         0.8660254]

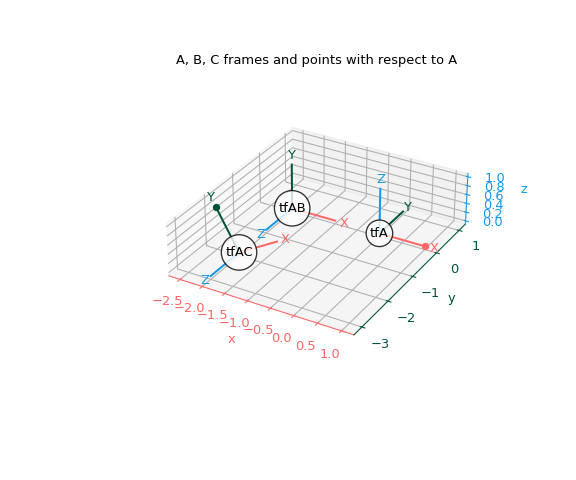
Постройте кадры относительно A снова, но также постройте эти две точки:

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_A, name="tfA")     # A plotted in A
>>> plot_transformed_axes(ax, tf_A_B, name="tfAB")  # B plotted in A
>>> plot_transformed_axes(ax, tf_A_C, name="tfAC")  # C plotted in A
>>> ax.scatter(p1_A[0], p1_A[1], p1_A[2], color=colors[0])  # +1 x_A
>>> ax.scatter(p2_A[0], p2_A[1], p2_A[2], color=colors[1])  # +1 y_C
>>> ax.set_title("A, B, C frames and points with respect to A")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

Переключение базовых систем отсчёта

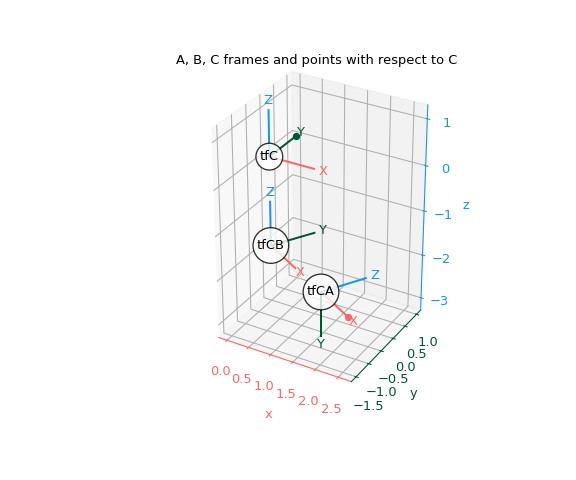
До этого момента мы визуализировали кадры с точки зрения A. Давайте используем определенные преобразования для визуализации кадров с точки зрения C.

Теперь C — это «базовая система координат» или «мировая система координат». Все системы координат являются тождественным преобразованием с их собственной точки зрения.

>>> tf_C = Tf.identity()

Мы уже определили преобразование C <- A и можем получить C <- B, инвертируя существующее преобразование B <- C.

>>> tf_C_B = tf_B_C.inv()  # C <- B

Это позволяет нам построить всё с точки зрения C:

>>> fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
>>> plot_transformed_axes(ax, tf_C, name="tfC")     # C plotted in C
>>> plot_transformed_axes(ax, tf_C_B, name="tfCB")  # B plotted in C
>>> plot_transformed_axes(ax, tf_C_A, name="tfCA")  # A plotted in C
>>> ax.scatter(p1_C[0], p1_C[1], p1_C[2], color=colors[0])
>>> ax.scatter(p2_C[0], p2_C[1], p2_C[2], color=colors[1])
>>> ax.set_title("A, B, C frames and points with respect to C")
>>> ax.set_aspect("equal")
>>> ax.figure.set_size_inches(6, 5)
>>> plt.show()

НазадОткрыть во вкладке