scipy.special.

diric

scipy.special.diric(x, n)

Периодическая функция sinc, также называемая функцией Дирихле.

Функция Дирихле определяется как:

diric(x, n) = sin(x * n/2) / (n * sin(x / 2)),

где n является положительным целым числом.

Параметры:

xarray_like

Входные данные

nint

Целое число, определяющее периодичность.

Возвращает:

diricndarray

Примеры

Попробуйте в вашем браузере!

>>> import numpy as np
>>> from scipy import special
>>> import matplotlib.pyplot as plt

>>> x = np.linspace(-8*np.pi, 8*np.pi, num=201)
>>> plt.figure(figsize=(8, 8));
>>> for idx, n in enumerate([2, 3, 4, 9]):
...     plt.subplot(2, 2, idx+1)
...     plt.plot(x, special.diric(x, n))
...     plt.title('diric, n={}'.format(n))
>>> plt.show()

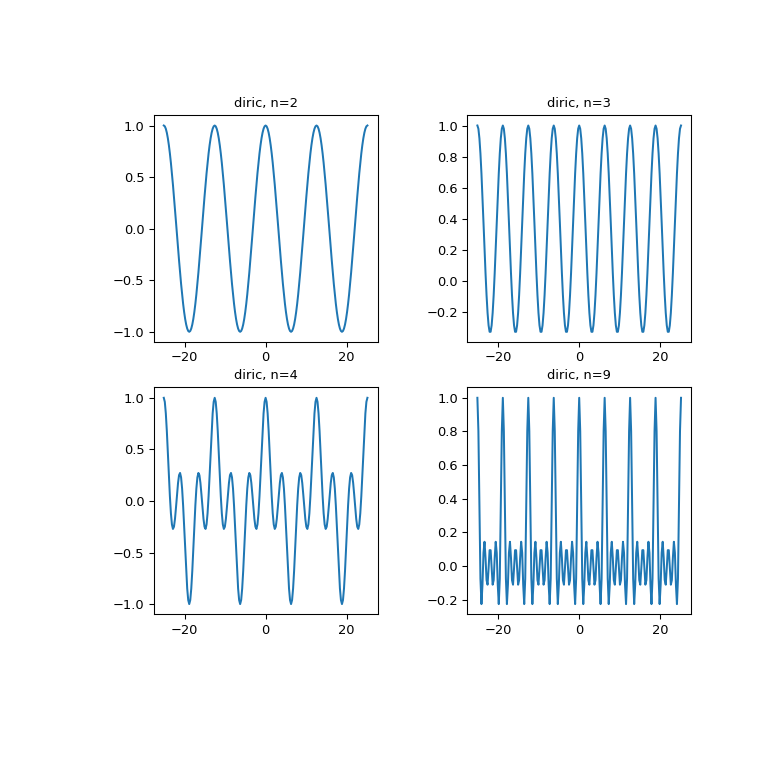
Следующий пример демонстрирует, что diric дает величины (по модулю знака и масштабирования) коэффициентов Фурье прямоугольного импульса.

Подавить вывод значений, которые эффективно равны 0:

>>> np.set_printoptions(suppress=True)

Создать сигнал x длины m с k единицы:

>>> m = 8
>>> k = 3
>>> x = np.zeros(m)
>>> x[:k] = 1

Использовать БПФ для вычисления преобразования Фурье от xи изучите величины коэффициентов:

>>> np.abs(np.fft.fft(x))
array([ 3.        ,  2.41421356,  1.        ,  0.41421356,  1.        ,
        0.41421356,  1.        ,  2.41421356])

Теперь найдите те же значения (с точностью до знака), используя diric. Мы умножаем на k для учёта различных соглашений о масштабировании numpy.fft.fft и diric:

>>> theta = np.linspace(0, 2*np.pi, m, endpoint=False)
>>> k * special.diric(theta, k)
array([ 3.        ,  2.41421356,  1.        , -0.41421356, -1.        ,
       -0.41421356,  1.        ,  2.41421356])

НазадОткрыть во вкладке