scipy.special.

jacobi

scipy.special.jacobi(n, alpha, beta, монический=False)

Полином Якоби.

Определяется как решение уравнения

\[(1 - x^2)\frac{d^2}{dx^2}P_n^{(\alpha, \beta)} + (\beta - \alpha - (\alpha + \beta + 2)x) \frac{d}{dx}P_n^{(\alpha, \beta)} + n(n + \alpha + \beta + 1)P_n^{(\alpha, \beta)} = 0\]

для \(\alpha, \beta > -1\); \(P_n^{(\alpha, \beta)}\) является полиномом степени \(n\).

Параметры:

nint

Степень полинома.

alphafloat

Параметр, должен быть больше -1.

betafloat

Параметр, должен быть больше -1.

моническийbool, необязательно

Если True, масштабировать старший коэффициент до 1. По умолчанию False.

Возвращает:

Porthopoly1d

Полином Якоби.

Примечания

Для фиксированного \(\alpha, \beta\), полиномы \(P_n^{(\alpha, \beta)}\) ортогональны на \([-1, 1]\) с весовой функцией \((1 - x)^\alpha(1 + x)^\beta\).

Ссылки

[AS]

Милтон Абрамовиц и Ирен А. Стегун, ред. Справочник по математическим функциям с формулами, графиками и математическими таблицами. Нью-Йорк: Dover, 1972.

Примеры

Попробуйте в вашем браузере!

Полиномы Якоби удовлетворяют рекуррентному соотношению:

\[P_n^{(\alpha, \beta-1)}(x) - P_n^{(\alpha-1, \beta)}(x) = P_{n-1}^{(\alpha, \beta)}(x)\]

Это можно проверить, например, для \(\alpha = \beta = 2\) и \(n = 1\) на интервале \([-1, 1]\):

>>> import numpy as np
>>> from scipy.special import jacobi
>>> x = np.arange(-1.0, 1.0, 0.01)
>>> np.allclose(jacobi(0, 2, 2)(x),
...             jacobi(1, 2, 1)(x) - jacobi(1, 1, 2)(x))
True

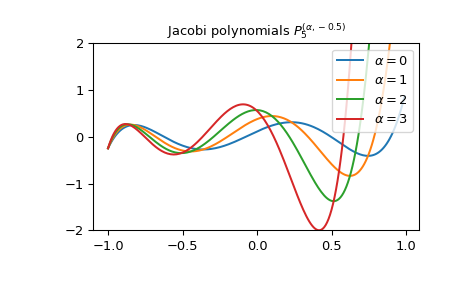
График полинома Якоби \(P_5^{(\alpha, -0.5)}\) для разных значений \(\alpha\):

>>> import matplotlib.pyplot as plt
>>> x = np.arange(-1.0, 1.0, 0.01)
>>> fig, ax = plt.subplots()
>>> ax.set_ylim(-2.0, 2.0)
>>> ax.set_title(r'Jacobi polynomials $P_5^{(\alpha, -0.5)}$')
>>> for alpha in np.arange(0, 4, 1):
...     ax.plot(x, jacobi(5, alpha, -0.5)(x), label=rf'$\alpha={alpha}$')
>>> plt.legend(loc='best')
>>> plt.show()

НазадОткрыть во вкладке