scipy.special.

y1p_zeros

scipy.special.y1p_zeros(nt, комплексный=False)

Вычислить nt нулей производной Бесселя Y1’(z) и значение в каждом нуле.

Значения задаются Y1(z1) в каждой точке z1, где Y1’(z1)=0.

Параметры:

ntint

Количество нулей для возврата

комплексныйbool, по умолчанию False

Установите False, чтобы возвращать только действительные нули; установите True, чтобы возвращать только комплексные нули с отрицательной действительной частью и положительной мнимой частью. Обратите внимание, что комплексно-сопряженные к последним также являются нулями функции, но не возвращаются этой процедурой.

Возвращает:

z1pnndarray

Расположение n-го нуля Y1’(z)

y1z1pnndarray

Значение производной Y1(z1) для n-го нуля

Ссылки

[1]

Zhang, Shanjie and Jin, Jianming. “Computation of Special Functions”, John Wiley and Sons, 1996, chapter 5. https://people.sc.fsu.edu/~jburkardt/f77_src/special_functions/special_functions.html

Примеры

Попробуйте в вашем браузере!

Вычислить первые четыре корня \(Y_1'\) и значения \(Y_1\) в этих корнях.

>>> import numpy as np
>>> from scipy.special import y1p_zeros
>>> y1grad_roots, y1_values = y1p_zeros(4)
>>> with np.printoptions(precision=5):
...     print(f"Y1' Roots: {y1grad_roots.real}")
...     print(f"Y1 values: {y1_values.real}")
Y1' Roots: [ 3.68302  6.9415  10.1234  13.28576]
Y1 values: [ 0.41673 -0.30317  0.25091 -0.21897]

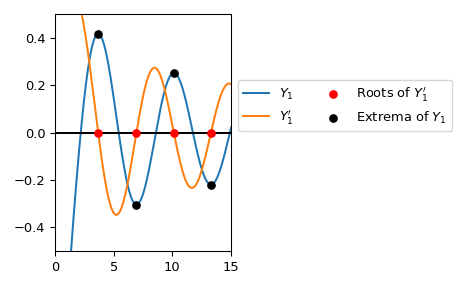
y1p_zeros может использоваться для вычисления экстремальных точек \(Y_1\) непосредственно. Здесь мы строим график \(Y_1\) и первые четыре экстремума.

>>> import matplotlib.pyplot as plt
>>> from scipy.special import y1, yvp
>>> y1_roots, y1_values_at_roots = y1p_zeros(4)
>>> real_roots = y1_roots.real
>>> xmax = 15
>>> x = np.linspace(0, xmax, 500)
>>> x[0] += 1e-15
>>> fig, ax = plt.subplots()
>>> ax.plot(x, y1(x), label=r'$Y_1$')
>>> ax.plot(x, yvp(1, x, 1), label=r"$Y_1'$")
>>> ax.scatter(real_roots, np.zeros((4, )), s=30, c='r',
...            label=r"Roots of $Y_1'$", zorder=5)
>>> ax.scatter(real_roots, y1_values_at_roots.real, s=30, c='k',
...            label=r"Extrema of $Y_1$", zorder=5)
>>> ax.hlines(0, 0, xmax, color='k')
>>> ax.set_ylim(-0.5, 0.5)
>>> ax.set_xlim(0, xmax)
>>> ax.legend(ncol=2, bbox_to_anchor=(1., 0.75))
>>> plt.tight_layout()
>>> plt.show()

НазадОткрыть во вкладке