scipy.stats.

linregress

scipy.stats.linregress(x, y, альтернатива='two-sided', *, ось=0, nan_policy='propagate', keepdims=False)

Вычисление линейной регрессии методом наименьших квадратов для двух наборов измерений.

Параметры:

x, yarray_like

Два набора измерений. Оба массива должны иметь одинаковую длину N.

альтернатива{‘two-sided’, ‘less’, ‘greater’}, необязательный

Определяет альтернативную гипотезу. По умолчанию 'two-sided'. Доступны следующие опции:

• ‘two-sided’: наклон линии регрессии ненулевой

• ‘less’: наклон линии регрессии меньше нуля

• 'greater': наклон линии регрессии больше нуля

Добавлено в версии 1.7.0.

осьint или None, по умолчанию: 0

Если это целое число, ось входных данных, по которой вычисляется статистика. Статистика каждого среза по оси (например, строки) входных данных появится в соответствующем элементе вывода. Если None, вход будет сведён в одномерный массив перед вычислением статистики.

nan_policy{‘propagate’, ‘omit’, ‘raise’}

Определяет, как обрабатывать входные значения NaN.

• propagate: если NaN присутствует в срезе оси (например, строке), вдоль которой вычисляется статистика, соответствующая запись вывода будет NaN.

• omit: NaN будут пропущены при выполнении расчета. Если в срезе оси, вдоль которого вычисляется статистика, остается недостаточно данных, соответствующая запись вывода будет NaN.

• raise: если присутствует NaN, то ValueError будет вызвано исключение.

keepdimsbool, по умолчанию: False

Если установлено значение True, оси, которые были сокращены, остаются в результате как размерности с размером один. С этой опцией результат будет корректно транслироваться относительно входного массива.

Возвращает:

результатLinregressResult экземпляр

Возвращаемое значение — объект со следующими атрибутами:

slopefloat

Наклон линии регрессии.

interceptfloat

Свободный член линии регрессии.

rvaluefloat

Коэффициент корреляции Пирсона. Квадрат rvalue равен коэффициенту детерминации.

p-значениеfloat

P-значение для проверки гипотезы, нулевая гипотеза которой состоит в том, что наклон равен нулю, с использованием критерия Вальда с t-распределением статистики критерия. См. альтернатива выше для альтернативных гипотез.

stderrfloat

Стандартная ошибка оценённого наклона (градиента), в предположении нормальности остатков.

intercept_stderrfloat

Стандартная ошибка оцененного пересечения, в предположении нормальности остатков.

Смотрите также

scipy.optimize.curve_fit

Использовать нелинейный метод наименьших квадратов для подгонки функции к данным.

scipy.optimize.leastsq

Минимизировать сумму квадратов набора уравнений.

Примечания

Для совместимости со старыми версиями SciPy возвращаемое значение ведёт себя как namedtuple длины 5, с полями slope, intercept, rvalue, pvalue и stderr, поэтому можно продолжать писать:

slope, intercept, r, p, se = linregress(x, y)

Однако при таком стиле стандартная ошибка пересечения не доступна. Чтобы иметь доступ ко всем вычисленным значениям, включая стандартную ошибку пересечения, используйте возвращаемое значение как объект с атрибутами, например:

result = linregress(x, y)
print(result.intercept, result.intercept_stderr)

Начиная с SciPy 1.9, np.matrix входные данные (не рекомендуется для нового кода) преобразуются в np.ndarray перед выполнением вычисления. В этом случае результатом будет скаляр или np.ndarray подходящей формы вместо 2D np.matrix. Аналогично, хотя маскированные элементы маскированных массивов игнорируются, результатом будет скаляр или np.ndarray вместо маскированного массива с mask=False.

Примеры

Попробуйте в вашем браузере!

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy import stats
>>> rng = np.random.default_rng()

Сгенерировать некоторые данные:

>>> x = rng.random(10)
>>> y = 1.6*x + rng.random(10)

Выполнить линейную регрессию:

>>> res = stats.linregress(x, y)

Коэффициент детерминации (R-квадрат):

>>> print(f"R-squared: {res.rvalue**2:.6f}")
R-squared: 0.717533

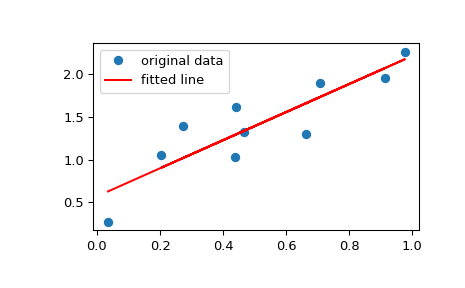
Постройте график данных вместе с подобранной линией:

>>> plt.plot(x, y, 'o', label='original data')
>>> plt.plot(x, res.intercept + res.slope*x, 'r', label='fitted line')
>>> plt.legend()
>>> plt.show()

Вычислить 95% доверительный интервал для наклона и пересечения:

>>> # Two-sided inverse Students t-distribution
>>> # p - probability, df - degrees of freedom
>>> from scipy.stats import t
>>> tinv = lambda p, df: abs(t.ppf(p/2, df))

>>> ts = tinv(0.05, len(x)-2)
>>> print(f"slope (95%): {res.slope:.6f} +/- {ts*res.stderr:.6f}")
slope (95%): 1.453392 +/- 0.743465
>>> print(f"intercept (95%): {res.intercept:.6f}"
...       f" +/- {ts*res.intercept_stderr:.6f}")
intercept (95%): 0.616950 +/- 0.544475

НазадОткрыть во вкладке