scipy.optimize.

curve_fit#

scipy.optimize.curve_fit(f, xdata, ydata, p0=None, sigma=None, absolute_sigma=False, check_finite=None, границы=(-inf, inf), метод=None, jac=None, *, full_output=False, nan_policy=None, **kwargs)[источник]#

Использовать нелинейный метод наименьших квадратов для подгонки функции f к данным.

Предполагает ydata = f(xdata, *params) + eps.

Параметры:

fcallable

Функция модели, f(x, …). Она должна принимать независимую переменную в качестве первого аргумента и параметры для подгонки в качестве отдельных оставшихся аргументов.

xdataarray_like

Независимая переменная, в которой измерены данные. Обычно должна быть последовательностью длины M или массивом формы (k,M) для функций с k предикторами, и каждый элемент должен быть преобразуемым в float, если это объект, подобный массиву.

ydataarray_like

Зависимые данные, массив длины M - номинально f(xdata, ...).

p0array_like, необязательный

Начальное приближение для параметров (длина N). Если None, то начальные значения будут все равны 1 (если количество параметров функции можно определить с помощью интроспекции, иначе вызывается ValueError).

sigmaNone или скаляр или последовательность длины M или массив MxM, опционально

Определяет неопределенность в ydata. Если мы определим остатки как r = ydata - f(xdata, *popt), тогда интерпретация sigma зависит от количества измерений:

Скаляр или 1-D sigma должны содержать значения стандартных отклонений ошибок в ydataВ этом случае оптимизируемая функция — chisq = sum((r / sigma) ** 2).
Двумерный sigma должна содержать ковариационную матрицу ошибок в ydataВ этом случае оптимизируемая функция — chisq = r.T @ inv(sigma) @ r.

Добавлено в версии 0.19.

None (по умолчанию) эквивалентно 1-D sigma заполнен единицами.

absolute_sigmabool, необязательно

Если True, sigma используется в абсолютном смысле, а оценённая ковариация параметров pcov отражает эти абсолютные значения.

Если False (по умолчанию), только относительные величины sigma значения имеют значение. Возвращаемая ковариационная матрица параметров pcov основан на масштабировании sigma на постоянный множитель. Эта константа устанавливается требованием, чтобы приведённый chisq для оптимальных параметров popt при использовании масштабированный sigma равна единице. Другими словами, sigma масштабируется для соответствия выборочной дисперсии остатков после подгонки. По умолчанию False. Математически, pcov(absolute_sigma=False) = pcov(absolute_sigma=True) * chisq(popt)/(M-N)

check_finitebool, необязательно

Если True, проверяет, что входные массивы не содержат nan или inf, и вызывает ValueError, если они есть. Установка этого параметра в False может молча привести к бессмысленным результатам, если входные массивы содержат nan. По умолчанию True, если nan_policy не указан явно, иначе False.

границы2-кортеж из array_like или Bounds, опционально

Нижние и верхние границы параметров. По умолчанию границы не заданы. Есть два способа указать границы:

Экземпляр Bounds класс.
2-кортеж из array_like: Каждый элемент кортежа должен быть либо массивом с длиной, равной количеству параметров, либо скаляром (в этом случае граница считается одинаковой для всех параметров). Используйте np.inf с соответствующим знаком для отключения ограничений на все или некоторые параметры.

метод{‘lm’, ‘trf’, ‘dogbox’}, опционально

Метод для использования в оптимизации. См. least_squares для получения дополнительных сведений. По умолчанию ‘lm’ для неограниченных задач и ‘trf’, если границы предоставлены. Метод 'lm' не будет работать, когда количество наблюдений меньше количества переменных, используйте 'trf' или 'dogbox' в этом случае.

Добавлено в версии 0.17.

jaccallable, string или None, опционально

Функция с сигнатурой jac(x, ...) которая вычисляет матрицу Якоби функции модели по параметрам как плотную структуру array_like. Она будет масштабирована в соответствии с предоставленными sigma. Если None (по умолчанию), матрица Якоби будет оценена численно. Строковые ключевые слова для методов ‘trf’ и ‘dogbox’ могут использоваться для выбора схемы конечных разностей, см. least_squares.

Добавлено в версии 0.18.

full_outputлогический, необязательный

Если True, эта функция возвращает дополнительную информацию: infodict, mesg, и ier.

Добавлено в версии 1.9.

nan_policy{‘raise’, ‘omit’, None}, опционально

Определяет, как обрабатывать входные данные, содержащие nan. Доступны следующие опции (по умолчанию None):

‘raise’: вызывает ошибку
'omit': выполняет вычисления, игнорируя значения nan
None: не выполняется специальная обработка NaN (кроме того, что делается check_finite); поведение при наличии NaN зависит от реализации и может измениться.

Обратите внимание, что если это значение указано явно (не None), check_finite будет установлено как False.

Добавлено в версии 1.11.

**kwargs

Аргументы ключевых слов, передаваемые в leastsq для method='lm' или least_squares в противном случае.

Возвращает:

poptмассив

Оптимальные значения параметров, чтобы сумма квадратов остатков f(xdata, *popt) - ydata минимизируется.

pcov2-D массив

Оценочная приближенная ковариация popt. Диагонали дают дисперсию оценки параметра. Чтобы вычислить ошибки в одно стандартное отклонение для параметров, используйте perr = np.sqrt(np.diag(pcov)). Обратите внимание, что связь между cov и оценки ошибок параметров выводятся на основе линейной аппроксимации функции модели в окрестности оптимума [1]. Когда это приближение становится неточным, cov может не давать точной меры неопределенности.

Как sigma параметр влияет на оценку ковариации зависит от absolute_sigma аргумент, как описано выше.

Если матрица Якоби в решении не имеет полного ранга, то метод 'lm' возвращает матрицу, заполненную np.inf, с другой стороны, методы 'trf' и 'dogbox' используют псевдообратную матрицу Мура-Пенроуза для вычисления ковариационной матрицы. Ковариационные матрицы с большими числами обусловленности (например, вычисленные с помощью numpy.linalg.cond) может указывать на то, что результаты ненадёжны.

infodictdict (возвращается только если full_output равно True)

словарь дополнительных выходных данных с ключами:

nfev: Количество вызовов функции. Методы 'trf' и 'dogbox' не учитывают вызовы функции для аппроксимации численного якобиана, в отличие от метода 'lm'.
fvec: Значения невязок, вычисленные в решении, для одномерного sigma это (f(x, *popt) - ydata)/sigma.
fjac: Перестановка матрицы R QR-разложения окончательной приближённой матрицы Якоби, хранимая по столбцам. Вместе с ipvt можно аппроксимировать ковариацию оценки. Только метод 'lm' предоставляет эту информацию.
ipvt: Целочисленный массив длины N, который определяет матрицу перестановки p, такую что fjac*p = q*r, где r — верхняя треугольная матрица с диагональными элементами неубывающей величины. Столбец j матрицы p — это столбец ipvt(j) единичной матрицы. Метод 'lm' предоставляет только эту информацию.
qtf: Вектор (transpose(q) * fvec). Метод 'lm' предоставляет только эту информацию.

Добавлено в версии 1.9.

mesgstr (возвращается только если full_output равно True)

Строковое сообщение с информацией о решении.

Добавлено в версии 1.9.

ierint (возвращается только если full_output равно True)

Целочисленный флаг. Если он равен 1, 2, 3 или 4, решение было найдено. В противном случае, решение не было найдено. В любом случае, дополнительная выходная переменная mesg даёт больше информации.

Добавлено в версии 1.9.

Вызывает:

ValueError: если любой из ydata или xdata содержат NaN или если используются несовместимые опции.
RuntimeError: если минимизация методом наименьших квадратов не удалась.
OptimizeWarning: если ковариацию параметров невозможно оценить.

Смотрите также

least_squares: Минимизировать сумму квадратов нелинейных функций.
scipy.stats.linregress: Вычислить линейную регрессию методом наименьших квадратов для двух наборов измерений.

Примечания

Пользователи должны убедиться, что входные данные xdata, ydata, и вывод f являются float64, иначе оптимизация может вернуть некорректные результаты.

С method='lm', алгоритм использует алгоритм Левенберга-Марквардта через leastsq. Обратите внимание, что этот алгоритм может работать только с неограниченными задачами.

Ограничения типа box могут обрабатываться методами 'trf' и 'dogbox'. См. строку документации least_squares для получения дополнительной информации.

Подбираемые параметры должны иметь схожий масштаб. Различия в несколько порядков величины могут привести к некорректным результатам. Для методов 'trf' и 'dogbox', x_scale ключевой аргумент может использоваться для масштабирования параметров.

curve_fit предназначен для локальной оптимизации параметров для минимизации суммы квадратов остатков. Для глобальной оптимизации, других вариантов целевой функции и других продвинутых функций рассмотрите использование Глобальная оптимизация инструменты или LMFIT пакет.

Ссылки

[1]

K. Vugrin и др. Методы оценки доверительных областей для нелинейной регрессии в потоке грунтовых вод: три примера. Water Resources Research, Vol. 43, W03423, DOI:10.1029/2005WR004804

Примеры

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from scipy.optimize import curve_fit

>>> def func(x, a, b, c):
...     return a * np.exp(-b * x) + c

Определите данные для аппроксимации с некоторым шумом:

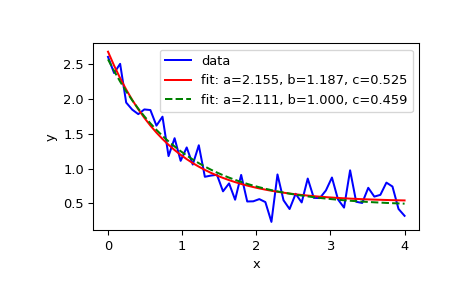
>>> xdata = np.linspace(0, 4, 50)
>>> y = func(xdata, 2.5, 1.3, 0.5)
>>> rng = np.random.default_rng()
>>> y_noise = 0.2 * rng.normal(size=xdata.size)
>>> ydata = y + y_noise
>>> plt.plot(xdata, ydata, 'b-', label='data')

Подгонка параметров a, b, c функции функция:

>>> popt, pcov = curve_fit(func, xdata, ydata)
>>> popt
array([2.56274217, 1.37268521, 0.47427475])
>>> plt.plot(xdata, func(xdata, *popt), 'r-',
...          label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))

Ограничить оптимизацию областью 0 <= a <= 3, 0 <= b <= 1 и 0 <= c <= 0.5:

>>> popt, pcov = curve_fit(func, xdata, ydata, bounds=(0, [3., 1., 0.5]))
>>> popt
array([2.43736712, 1.        , 0.34463856])
>>> plt.plot(xdata, func(xdata, *popt), 'g--',
...          label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))

>>> plt.xlabel('x')
>>> plt.ylabel('y')
>>> plt.legend()
>>> plt.show()

../../_images/scipy-optimize-curve_fit-1_00_00.png

Для надежных результатов модель функция не должен быть перепараметризован; избыточные параметры могут привести к ненадёжным ковариационным матрицам и, в некоторых случаях, к ухудшению качества подгонки. Для быстрой проверки, не перепараметризована ли модель, вычислите число обусловленности ковариационной матрицы:

>>> np.linalg.cond(pcov)
34.571092161547405  # may vary

Значение мало, поэтому не вызывает особого беспокойства. Однако, если бы мы добавили четвёртый параметр d to функция с тем же эффектом, что и a:

>>> def func2(x, a, b, c, d):
...     return a * d * np.exp(-b * x) + c  # a and d are redundant
>>> popt, pcov = curve_fit(func2, xdata, ydata)
>>> np.linalg.cond(pcov)
1.13250718925596e+32  # may vary

Такое большое значение вызывает беспокойство. Диагональные элементы матрицы ковариации, которая связана с неопределенностью подгонки, дают больше информации:

>>> np.diag(pcov)
array([1.48814742e+29, 3.78596560e-02, 5.39253738e-03, 2.76417220e+28])  # may vary

Обратите внимание, что первый и последний члены значительно больше остальных элементов, что указывает на неоднозначность оптимальных значений этих параметров и на то, что только один из этих параметров необходим в модели.

Если оптимальные параметры f отличаются на несколько порядков величины, результирующая аппроксимация может быть неточной. Иногда, curve_fit может не найти результатов:

>>> ydata = func(xdata, 500000, 0.01, 15)
>>> try:
...     popt, pcov = curve_fit(func, xdata, ydata, method = 'trf')
... except RuntimeError as e:
...     print(e)
Optimal parameters not found: The maximum number of function evaluations is
exceeded.

Если параметр scale примерно известен заранее, он может быть определён в x_scale аргумент:

>>> popt, pcov = curve_fit(func, xdata, ydata, method = 'trf',
...                        x_scale = [1000, 1, 1])
>>> popt
array([5.00000000e+05, 1.00000000e-02, 1.49999999e+01])