scipy.stats.

logrank#

scipy.stats.logrank(x, y, альтернатива='two-sided')[источник]#

Сравнить распределения выживаемости двух выборок с помощью логранк-теста.

Параметры:

x, yarray_like или CensoredData

Выборки для сравнения на основе их эмпирических функций выживания.

альтернатива{‘two-sided’, ‘less’, ‘greater’}, необязательный

Определяет альтернативную гипотезу.

Нулевая гипотеза состоит в том, что функции выживания двух групп, скажем X и Y, идентичны.

Следующие альтернативные гипотезы [4] доступны (по умолчанию «two-sided»):

'two-sided': функции выживания двух групп не идентичны.
‘less’: выживаемость группы X предпочтительнее: группа X функция интенсивности отказов меньше, чем группа Y функция интенсивности отказов в некоторые моменты времени.
‘greater’: выживание группы Y предпочтительнее: группа X функция интенсивности отказов больше, чем у группы Y функция интенсивности отказов в некоторые моменты времени.

Возвращает:

resLogRankResult

Объект, содержащий атрибуты:

статистикаfloat ndarray: Вычисленная статистика (определена ниже). Её величина — это квадратный корень величины, возвращаемой большинством других реализаций теста логранга.
p-значениеfloat ndarray: Вычисленное p-значение теста.

Смотрите также

scipy.stats.ecdf

Примечания

Тест логранга [1] сравнивает наблюдаемое количество событий с ожидаемым количеством событий при нулевой гипотезе, что две выборки были взяты из одного распределения. Статистика равна

\[Z_i = \frac{\sum_{j=1}^J(O_{i,j}-E_{i,j})}{\sqrt{\sum_{j=1}^J V_{i,j}}} \rightarrow \mathcal{N}(0,1)\]

где

\[E_{i,j} = O_j \frac{N_{i,j}}{N_j}, \qquad V_{i,j} = E_{i,j} \left(\frac{N_j-O_j}{N_j}\right) \left(\frac{N_j-N_{i,j}}{N_j-1}\right),\]

\(i\) обозначает группу (т.е. может принимать значения \(x\) или \(y\), или он может быть опущен для ссылки на объединённую выборку) \(j\) обозначает время (в которое произошло событие), \(N\) это количество субъектов в группе риска непосредственно перед наступлением события, и \(O\) это наблюдаемое количество событий в это время.

The statistic \(Z_x\) возвращаемый logrank — это (знаковый) квадратный корень статистики, возвращаемой многими другими реализациями. При нулевой гипотезе \(Z_x**2\) асимптотически распределен согласно хи-квадрат распределению с одной степенью свободы. Следовательно, \(Z_x\) асимптотически распределена в соответствии со стандартным нормальным распределением. Преимущество использования \(Z_x\) сохраняется ли знак информации (т.е. имеет ли наблюдаемое количество событий тенденцию быть меньше или больше ожидаемого количества при нулевой гипотезе), что позволяет scipy.stats.logrank для предложения односторонних альтернативных гипотез.

Ссылки

[1]

Мантел Н. "Оценка данных выживаемости и две новые статистики рангового порядка, возникающие при ее рассмотрении." Cancer Chemotherapy Reports, 50(3):163-170, PMID: 5910392, 1966

[2]

Блэнд, Олтман, "Тест логранка", BMJ, 328:1073, DOI:10.1136/bmj.328.7447.1073, 2004

[3]

“Logrank test”, Википедия, https://en.wikipedia.org/wiki/Logrank_test

[4]

Brown, Mark. “On the choice of variance for the log rank test.” Biometrika 71.1 (1984): 65-74.

[5]

Клайн, Джон П., и Мелвин Л. Мошбергер. Анализ выживаемости: методы для цензурированных и усечённых данных. Том 1230. Нью-Йорк: Springer, 2003.

Примеры

Ссылка [2] сравнил время выживания пациентов с двумя разными типами рецидивирующих злокачественных глиом. Образцы ниже записывают время (количество недель), в течение которого каждый пациент участвовал в исследовании. scipy.stats.CensoredData класс используется, потому что данные являются правоцензурированными: нецензурированные наблюдения соответствуют наблюдаемым смертям, тогда как цензурированные наблюдения соответствуют случаям, когда пациент покинул исследование по другой причине.

>>> from scipy import stats
>>> x = stats.CensoredData(
...     uncensored=[6, 13, 21, 30, 37, 38, 49, 50,
...                 63, 79, 86, 98, 202, 219],
...     right=[31, 47, 80, 82, 82, 149]
... )
>>> y = stats.CensoredData(
...     uncensored=[10, 10, 12, 13, 14, 15, 16, 17, 18, 20, 24, 24,
...                 25, 28,30, 33, 35, 37, 40, 40, 46, 48, 76, 81,
...                 82, 91, 112, 181],
...     right=[34, 40, 70]
... )

Мы можем вычислить и визуализировать эмпирические функции выживания обеих групп следующим образом.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> ax = plt.subplot()
>>> ecdf_x = stats.ecdf(x)
>>> ecdf_x.sf.plot(ax, label='Astrocytoma')
>>> ecdf_y = stats.ecdf(y)
>>> ecdf_y.sf.plot(ax, label='Glioblastoma')
>>> ax.set_xlabel('Time to death (weeks)')
>>> ax.set_ylabel('Empirical SF')
>>> plt.legend()
>>> plt.show()

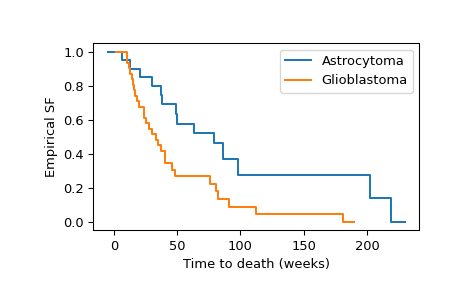
../../_images/scipy-stats-logrank-1_00_00.png

Визуальный анализ эмпирических функций выживания предполагает, что времена выживания имеют тенденцию различаться между двумя группами. Для формальной оценки значимости различия на уровне 1% используем логарифмический ранговый критерий.

>>> res = stats.logrank(x=x, y=y)
>>> res.statistic
-2.73799
>>> res.pvalue
0.00618

P-значение меньше 1%, поэтому мы можем считать данные свидетельством против нулевой гипотезы в пользу альтернативы о наличии разницы между двумя функциями выживаемости.