scipy.stats.

ecdf

scipy.stats.ecdf(sample)

Эмпирическая функция распределения выборки.

Эмпирическая функция распределения (ECDF) — это ступенчатая функция, оценивающая CDF распределения, лежащего в основе выборки. Эта функция возвращает объекты, представляющие как эмпирическую функцию распределения, так и её дополнение — эмпирическую функцию выживания.

Параметры:

sample1D array_like или scipy.stats.CensoredData

Помимо array_like, экземпляры scipy.stats.CensoredData поддерживаются нецензурированные и правоцензурированные наблюдения. В настоящее время другие экземпляры scipy.stats.CensoredData приведёт к NotImplementedError.

Возвращает:

resECDFResult

Объект со следующими атрибутами.

функция распределенияEmpiricalDistributionFunction

Объект, представляющий эмпирическую функцию кумулятивного распределения.

sfEmpiricalDistributionFunction

Объект, представляющий эмпирическую функцию выживания.

The функция распределения и sf сами атрибуты имеют следующие атрибуты.

quantilesndarray

Уникальные значения в выборке, определяющие эмпирическую CDF/SF.

вероятностиndarray

Точечные оценки вероятностей, соответствующих quantiles.

И следующие методы:

evaluate(x) :

Вычислить CDF/SF при аргументе.

plot(ax) :

Построить CDF/SF на предоставленных осях.

confidence_interval(confidence_level=0.95) :

Вычислить доверительный интервал вокруг функции распределения/функции выживания при значениях в quantiles.

Примечания

Когда каждое наблюдение выборки является точным измерением, эмпирическая функция распределения увеличивается на 1/len(sample) в каждой из наблюдений [1].

Когда наблюдения являются нижними границами, верхними границами или одновременно верхними и нижними границами, данные называются "цензурированными", и sample может быть предоставлен как экземпляр scipy.stats.CensoredData.

Для право-цензурированных данных ECDF задаётся оценкой Каплана-Мейера [2]другие формы цензурирования в настоящее время не поддерживаются.

Доверительные интервалы вычисляются по формуле Гринвуда или более современной формуле "Экспоненциальный Гринвуд", как описано в [4].

Ссылки

[1] (1,2,3)

Conover, William Jay. Practical nonparametric statistics. Vol. 350. John Wiley & Sons, 1999.

[2]

Kaplan, Edward L., and Paul Meier. “Nonparametric estimation from incomplete observations.” Journal of the American statistical association 53.282 (1958): 457-481.

[3]

Гоэл, Маниш Кумар, Пардип Ханна и Джугал Кишор. «Понимание анализа выживаемости: оценка Каплана-Мейера». International journal of Ayurveda research 1.4 (2010): 274.

[4]

Sawyer, Stanley. “The Greenwood and Exponential Greenwood Confidence Intervals in Survival Analysis.” https://www.math.wustl.edu/~sawyer/handouts/greenwood.pdf

Примеры

Попробуйте в вашем браузере!

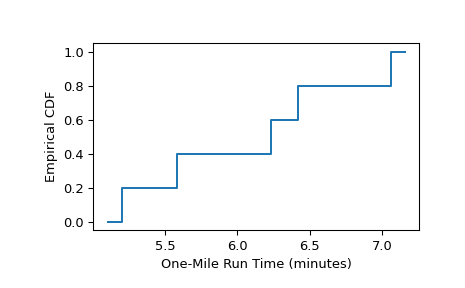
Нецензурированные данные

Как в примере из [1] страница 79, пять мальчиков были выбраны случайным образом из учащихся одной старшей школы. Их время пробега одной мили было записано следующим образом.

>>> sample = [6.23, 5.58, 7.06, 6.42, 5.20]  # one-mile run times (minutes)

Эмпирическая функция распределения, которая аппроксимирует функцию распределения времени пробега одной мили для популяции, из которой были взяты мальчики, вычисляется следующим образом.

>>> from scipy import stats
>>> res = stats.ecdf(sample)
>>> res.cdf.quantiles
array([5.2 , 5.58, 6.23, 6.42, 7.06])
>>> res.cdf.probabilities
array([0.2, 0.4, 0.6, 0.8, 1. ])

Чтобы построить результат как ступенчатую функцию:

>>> import matplotlib.pyplot as plt
>>> ax = plt.subplot()
>>> res.cdf.plot(ax)
>>> ax.set_xlabel('One-Mile Run Time (minutes)')
>>> ax.set_ylabel('Empirical CDF')
>>> plt.show()

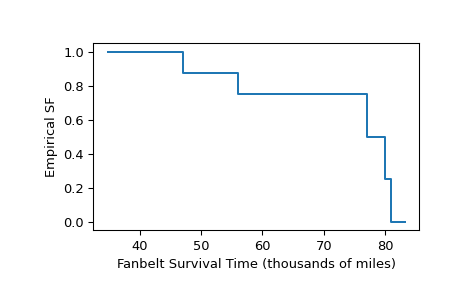
Право-цензурированные данные

Как в примере из [1] страница 91, были протестированы сроки службы десяти автомобильных ремней вентилятора. Пять тестов завершились из-за разрыва тестируемого ремня, но остальные тесты завершились по другим причинам (например, закончилось финансирование исследования, но ремень всё ещё был функционален). Пробег с ремнями был записан следующим образом.

>>> broken = [77, 47, 81, 56, 80]  # in thousands of miles driven
>>> unbroken = [62, 60, 43, 71, 37]

Точное время выживания ремней вентилятора, которые всё ещё были функциональны в конце тестов, неизвестно, но известно, что они превышают значения, записанные в unbroken. Следовательно, эти наблюдения называются «право-цензурированными», и данные представлены с использованием scipy.stats.CensoredData.

>>> sample = stats.CensoredData(uncensored=broken, right=unbroken)

Эмпирическая функция выживания рассчитывается следующим образом.

>>> res = stats.ecdf(sample)
>>> res.sf.quantiles
array([37., 43., 47., 56., 60., 62., 71., 77., 80., 81.])
>>> res.sf.probabilities
array([1.   , 1.   , 0.875, 0.75 , 0.75 , 0.75 , 0.75 , 0.5  , 0.25 , 0.   ])

Чтобы построить результат как ступенчатую функцию:

>>> ax = plt.subplot()
>>> res.sf.plot(ax)
>>> ax.set_xlabel('Fanbelt Survival Time (thousands of miles)')
>>> ax.set_ylabel('Empirical SF')
>>> plt.show()

НазадОткрыть во вкладке