scipy.stats.

monte_carlo_test#

scipy.stats.monte_carlo_test(данные, rvs, статистика, *, векторизованный=None, n_resamples=9999, batch=None, альтернатива='two-sided', ось=0)[источник]#

Выполнить тест гипотезы методом Монте-Карло.

данные содержит выборку или последовательность одной или нескольких выборок. rvs определяет распределение(я) выборки(ок) в данные при нулевой гипотезе. Значение статистика для заданного данные сравнивается с нулевым распределением Монте-Карло: значение статистики для каждого из n_resamples наборы выборок, сгенерированные с использованием rvs. Это даёт p-значение, вероятность наблюдения такого экстремального значения тестовой статистики при нулевой гипотезе.

Параметры:

данныеarray-like или последовательность array-like

Массив или последовательность массивов наблюдений.

rvsвызываемый объект или кортеж вызываемых объектов

Вызываемый объект или последовательность вызываемых объектов, генерирующих случайные величины при нулевой гипотезе. Каждый элемент rvs должен быть вызываемым объектом, который принимает аргумент ключевого слова size (например, rvs(size=(m, n))) и возвращает N-мерный массив выборки такой формы. Если rvs является последовательностью, количество вызываемых объектов в rvs должно соответствовать количеству образцов в данные, т.е. len(rvs) == len(data). Если rvs является единым вызываемым объектом, данные рассматривается как единый образец.

статистикаcallable

Статистика, для которой вычисляется p-значение проверки гипотезы. статистика должен быть вызываемым объектом, принимающим выборку (например, statistic(sample)) или len(rvs) отдельные выборки (например, statistic(samples1, sample2) if rvs содержит два вызываемых объекта и данные содержит две выборки) и возвращает результирующую статистику. Если векторизованный установлен True, статистика также должен принимать аргумент-ключевое слово ось и векторизован для вычисления статистики вдоль предоставленной ось выборок в данные.

векторизованныйbool, необязательно

Если векторизованный установлен False, статистика не будет передан именованный аргумент ось и ожидается, что она вычисляет статистику только для одномерных выборок. Если True, статистика будет передан аргумент ключевого слова ось и ожидается, что он вычислит статистику вдоль ось при передаче ND-массивов выборки. Если None (по умолчанию), векторизованный будет установлено True if axis является параметром статистика. Использование векторизованной статистики обычно сокращает время вычислений.

n_resamplesint, по умолчанию: 9999

Количество выборок, взятых из каждого вызываемого объекта rvs. Эквивалентно, количество статистических значений при нулевой гипотезе, используемое как распределение нулевой гипотезы Монте-Карло.

batchint, необязательный

Количество выборок Монте-Карло для обработки в каждом вызове статистика. Использование памяти составляет O( batch * sample.size[axis] ). По умолчанию равно None, в этом случае batch равно n_resamples.

альтернатива{‘two-sided’, ‘less’, ‘greater’}

Альтернативная гипотеза, для которой рассчитывается p-значение. Для каждой альтернативы p-значение определяется следующим образом.

'greater' : процент нулевого распределения, который больше или равен наблюдаемому значению тестовой статистики.
'less' : процент нулевого распределения, который меньше или равен наблюдаемому значению статистики критерия.
'two-sided' : удвоенное меньшее из p-значений выше.

осьint, по умолчанию: 0

Ось данные (или каждый образец в данные) по которому рассчитывается статистика.

Возвращает:

resMonteCarloTestResult

Объект с атрибутами:

статистикаfloat или ndarray: Тестовая статистика наблюдаемого данные.
p-значениеfloat или ndarray: P-значение для данной альтернативы.
null_distributionndarray: Значения тестовой статистики, сгенерированные при нулевой гипотезе.

Предупреждение

P-значение рассчитывается путем подсчета элементов нулевого распределения, которые являются такими же или более экстремальными, чем наблюдаемое значение статистики. Из-за использования арифметики с конечной точностью некоторые статистические функции возвращают численно различные значения, когда теоретические значения были бы точно равны. В некоторых случаях это может привести к большой ошибке в рассчитанном p-значении. monte_carlo_test защищает от этого, рассматривая элементы в нулевом распределении, которые «близки» (в пределах относительного допуска в 100 раз больше эпсилон с плавающей запятой для неточных типов данных) к наблюдаемому значению тестовой статистики, как равные наблюдаемому значению тестовой статистики. Однако пользователю рекомендуется проверить нулевое распределение, чтобы оценить, подходит ли этот метод сравнения, и если нет, рассчитать p-значение вручную.

Ссылки

[1]

B. Phipson и G. K. Smyth. "Permutation P-values Should Never Be Zero: Calculating Exact P-values When Permutations Are Randomly Drawn." Statistical Applications in Genetics and Molecular Biology 9.1 (2010).

Примеры

Предположим, мы хотим проверить, была ли небольшая выборка взята из нормального распределения. Мы решаем использовать асимметрию выборки в качестве тестовой статистики и будем считать p-значение 0.05 статистически значимым.

>>> import numpy as np
>>> from scipy import stats
>>> def statistic(x, axis):
...     return stats.skew(x, axis)

После сбора данных мы вычисляем наблюдаемое значение тестовой статистики.

>>> rng = np.random.default_rng()
>>> x = stats.skewnorm.rvs(a=1, size=50, random_state=rng)
>>> statistic(x, axis=0)
0.12457412450240658

Чтобы определить вероятность наблюдения такого экстремального значения асимметрии случайно, если выборка была взята из нормального распределения, мы можем выполнить тест Монте-Карло. Тест будет случайным образом извлекать множество выборок из их нормального распределения, вычислять асимметрию каждой выборки и сравнивать нашу исходную асимметрию с этим распределением для определения приблизительного p-значения.

>>> from scipy.stats import monte_carlo_test
>>> # because our statistic is vectorized, we pass `vectorized=True`
>>> rvs = lambda size: stats.norm.rvs(size=size, random_state=rng)
>>> res = monte_carlo_test(x, rvs, statistic, vectorized=True)
>>> print(res.statistic)
0.12457412450240658
>>> print(res.pvalue)
0.7012

Вероятность получения тестовой статистики, меньшей или равной наблюдаемому значению при нулевой гипотезе, составляет ~70%. Это больше нашего выбранного порога в 5%, поэтому мы не можем считать это значимым свидетельством против нулевой гипотезы.

Обратите внимание, что это p-значение по сути совпадает с scipy.stats.skewtest, который опирается на асимптотическое распределение тестовой статистики, основанной на выборочной асимметрии.

>>> stats.skewtest(x).pvalue
0.6892046027110614

Эта асимптотическая аппроксимация недействительна для малых размеров выборки, но monte_carlo_test может использоваться с выборками любого размера.

>>> x = stats.skewnorm.rvs(a=1, size=7, random_state=rng)
>>> # stats.skewtest(x) would produce an error due to small sample
>>> res = monte_carlo_test(x, rvs, statistic, vectorized=True)

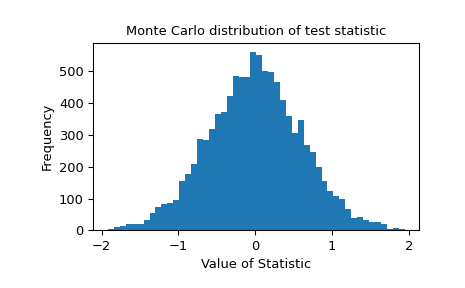
Распределение Монте-Карло тестовой статистики предоставлено для дальнейшего исследования.

>>> import matplotlib.pyplot as plt
>>> fig, ax = plt.subplots()
>>> ax.hist(res.null_distribution, bins=50)
>>> ax.set_title("Monte Carlo distribution of test statistic")
>>> ax.set_xlabel("Value of Statistic")
>>> ax.set_ylabel("Frequency")
>>> plt.show()

../../_images/scipy-stats-monte_carlo_test-1.png