scipy.stats.

permutation_test

scipy.stats.permutation_test(данные, статистика, *, permutation_type='independent', векторизованный=None, n_resamples=9999, batch=None, альтернатива='two-sided', ось=0, rng=None, random_state=None)

Выполняет перестановочный тест заданной статистики на предоставленных данных.

Для независимой статистики выборок нулевая гипотеза состоит в том, что данные случайно выбраны из одного распределения. Для парной статистики выборок можно проверить две нулевые гипотезы: что данные спарены случайным образом или что данные случайно назначены выборкам.

Параметры:

данныеитерируемый объект из array-like

Содержит выборки, каждая из которых представляет собой массив наблюдений. Размерности массивов выборок должны быть совместимы для вещания, за исключением вдоль ось.

статистикаcallable

Статистика, для которой вычисляется p-значение проверки гипотезы. статистика должен быть вызываемым объектом, который принимает образцы в качестве отдельных аргументов (например, statistic(*data)) и возвращает полученную статистику. Если векторизованный установлен True, статистика также должен принимать аргумент-ключевое слово ось и векторизован для вычисления статистики вдоль предоставленной ось массивов выборки.

permutation_type{‘independent’, ‘samples’, ‘pairings’}, опционально

Тип перестановок, которые должны быть выполнены, в соответствии с нулевой гипотезой. Первые два типа перестановок предназначены для парных выборочных статистик, в которых все выборки содержат одинаковое количество наблюдений, а наблюдения с соответствующими индексами вдоль ось считаются парными; третий предназначен для статистики независимых выборок.

• 'samples' : наблюдения назначаются разным выборкам, но остаются парными с теми же наблюдениями из других выборок. Этот тип перестановки подходит для парных выборочных гипотезных тестов, таких как критерий знаковых рангов Уилкоксона и парный t-тест.

• 'pairings' : наблюдения сопоставляются с разными наблюдениями, но они остаются в той же выборке. Этот тип перестановки подходит для тестов ассоциации/корреляции со статистиками, такими как коэффициент Спирмена \(\rho\), Кендалла \(\tau\), и Пирсона \(r\).

• 'independent' (по умолчанию): наблюдения назначаются разным выборкам. Выборки могут содержать разное количество наблюдений. Этот тип перестановки подходит для тестов гипотез независимых выборок, таких как тест Манна-Уитни \(U\) тест и независимый t-тест для выборки.

  Пожалуйста, ознакомьтесь с разделом Примечания ниже для более подробных описаний типов перестановок.

векторизованныйbool, необязательно

Если векторизованный установлен False, статистика не будет передан именованный аргумент ось и ожидается, что она вычисляет статистику только для одномерных выборок. Если True, статистика будет передан аргумент ключевого слова ось и ожидается, что он вычислит статистику вдоль ось при передаче ND-массива выборки. Если None (по умолчанию), векторизованный будет установлено True if axis является параметром статистика. Использование векторизованной статистики обычно сокращает время вычислений.

n_resamplesint или np.inf, по умолчанию: 9999

Количество случайных перестановок (ресэмплов), используемых для аппроксимации нулевого распределения. Если больше или равно количеству различных перестановок, будет вычислено точное нулевое распределение. Обратите внимание, что количество различных перестановок растёт очень быстро с размерами выборок, поэтому точные тесты возможны только для очень маленьких наборов данных.

batchint, необязательный

Количество перестановок для обработки в каждом вызове статистикаИспользование памяти составляет O( batch * n ), где n — это общий размер всех выборок, независимо от значения векторизованный. По умолчанию None, в этом случае batch — это количество перестановок.

альтернатива{‘two-sided’, ‘less’, ‘greater’}, необязательный

Альтернативная гипотеза, для которой вычисляется p-значение. Для каждой альтернативы p-значение определяется для точных тестов следующим образом.

• 'greater' : процент нулевого распределения, который больше или равен наблюдаемому значению тестовой статистики.

• 'less' : процент нулевого распределения, который меньше или равен наблюдаемому значению статистики критерия.

• 'two-sided' (по умолчанию) : удвоенное меньшее из p-значений выше.

Обратите внимание, что p-значения для рандомизированных тестов рассчитываются в соответствии с консервативным (завышенным) приближением, предложенным в [2] и [3] вместо несмещённой оценки, предложенной в [4]. То есть, при расчете доли рандомизированного нулевого распределения, которая является такой же экстремальной, как наблюдаемое значение тестовой статистики, значения в числителе и знаменателе оба увеличиваются на единицу. Интерпретация этой поправки заключается в том, что наблюдаемое значение тестовой статистики всегда включается как элемент рандомизированного нулевого распределения. Используемое соглашение для двусторонних p-значений не является универсальным; наблюдаемая тестовая статистика и нулевое распределение возвращаются на случай, если предпочтительно другое определение.

осьint, по умолчанию: 0

Ось (расширенных) выборок, по которой вычисляется статистика. Если выборки имеют разное количество измерений, одноэлементные измерения добавляются к выборкам с меньшим количеством измерений перед ось рассматривается.

rng{None, int, numpy.random.Generator, опционально

Если rng передается по ключевому слову, типы, отличные от numpy.random.Generator передаются в numpy.random.default_rng для создания экземпляра Generator. Если rng уже является Generator экземпляр, то предоставленный экземпляр используется. Укажите rng для повторяемого поведения функции.

Если этот аргумент передаётся по позиции или random_state передается по ключевому слову, устаревшее поведение для аргумента random_state применяется:

• Если random_state равно None (или numpy.random), numpy.random.RandomState используется синглтон.

• Если random_state является int, новый RandomState используется экземпляр, инициализированный с random_state.

• Если random_state уже является Generator или RandomState экземпляр, тогда этот экземпляр используется.

Изменено в версии 1.15.0: В рамках SPEC-007 переход от использования numpy.random.RandomState to numpy.random.Generator, этот ключевое слово было изменено с random_state to rng. В переходный период оба ключевых слова будут продолжать работать, хотя только одно может быть указано за раз. После переходного периода вызовы функций, использующие random_state ключевое слово будет выдавать предупреждения. Поведение обоих random_state и rng описаны выше, но только rng ключевое слово должно использоваться в новом коде.

Возвращает:

resPermutationTestResult

Объект с атрибутами:

статистикаfloat или ndarray

Наблюдаемая тестовая статистика данных.

p-значениеfloat или ndarray

P-значение для данной альтернативы.

null_distributionndarray

Значения тестовой статистики, сгенерированные при нулевой гипотезе.

Примечания

Три типа перестановочных тестов, поддерживаемых этой функцией, описаны ниже.

Непарная статистика (permutation_type='independent'):

Нулевая гипотеза, связанная с этим типом перестановки, заключается в том, что все наблюдения взяты из одного и того же базового распределения и были случайным образом назначены одной из выборок.

Предположим data содержит две выборки; например. a, b = data. Когда 1 < n_resamples < binom(n, k), где

• k это количество наблюдений в a,

• n является общим числом наблюдений в a и b, и

• binom(n, k) это биномиальный коэффициент (n выбрать k),

данные объединяются (конкатенируются), случайным образом назначаются либо первой, либо второй выборке, и вычисляется статистика. Этот процесс выполняется многократно, был удален из основного пространства имен. Используйте раз, генерируя распределение статистики при нулевой гипотезе. Статистика исходных данных сравнивается с этим распределением для определения p-значения.

Когда n_resamples >= binom(n, k), выполняется точный тест: данные разделённый между выборками каждым различным способом ровно один раз, и точное нулевое распределение формируется. Обратите внимание, что для заданного разделения данных между выборками, только одно упорядочение/перестановка данных внутри каждый образец учитывается. Для статистик, которые не зависят от порядка данных внутри образцов, это значительно снижает вычислительные затраты без влияния на форму нулевого распределения (поскольку частота/количество каждого значения изменяется на тот же коэффициент).

Для a = [a1, a2, a3, a4] и b = [b1, b2, b3], пример этого типа перестановки x = [b3, a1, a2, b2] и y = [a4, b1, a3]. Поскольку используется только одно упорядочивание/перестановка данных внутри каждый образец рассматривается в точном тесте, ресемплинг как x = [b3, a1, b2, a2] и y = [a4, a3, b1] будет не следует считать отличным от приведённого выше примера.

permutation_type='independent' не поддерживает одновыборочную статистику, но может применяться к статистике с более чем двумя выборками. В этом случае, если n является массивом количества наблюдений в каждой выборке, количество различных разбиений равно:

np.prod([binom(sum(n[i:]), sum(n[i+1:])) for i in range(len(n)-1)])

Парная статистика, перестановка пар (permutation_type='pairings'):

Нулевая гипотеза, связанная с этим типом перестановки, заключается в том, что наблюдения в каждой выборке взяты из одного и того же базового распределения, а пары с элементами других выборок назначаются случайным образом.

Предположим data содержит только один образец; например. a, = data, и мы хотим рассмотреть все возможные пары элементов из a с элементами второго образца, b. Пусть n будет количеством наблюдений в a, что также должно равняться количеству наблюдений в b.

Когда 1 < n_resamples < factorial(n), элементы a случайно переставляются. Пользовательская статистика принимает один аргумент данных, скажем a_perm, и вычисляет статистику, учитывая a_perm и b. Этот процесс выполняется повторно, был удален из основного пространства имен. Используйте раз, генерируя распределение статистики при нулевой гипотезе. Статистика исходных данных сравнивается с этим распределением для определения p-значения.

Когда n_resamples >= factorial(n), выполняется точный тест: a переставляется каждым различным способом ровно один раз. Следовательно, статистика вычисляется для каждой уникальной пары образцов между a и b ровно один раз.

Для a = [a1, a2, a3] и b = [b1, b2, b3], пример этого типа перестановки a_perm = [a3, a1, a2] в то время как b остается в исходном порядке.

permutation_type='pairings' поддерживает data содержащий любое количество выборок, каждая из которых должна содержать одинаковое количество наблюдений. Все выборки, предоставленные в data переставлены независимо. Следовательно, если m — это количество образцов и n является количеством наблюдений в каждой выборке, тогда количество перестановок в точном тесте равно:

factorial(n)**m

Обратите внимание, что если статистика для двух выборок, например, не зависит по своей природе от порядка предоставления наблюдений — только от pairings наблюдений - тогда только одна из двух выборок должна быть предоставлена в data. Это значительно снижает вычислительные затраты, не влияя на форму нулевого распределения (поскольку частота/количество каждого значения изменяется на тот же коэффициент).

Парная статистика, перестановка выборок (permutation_type='samples'):

Нулевая гипотеза, связанная с этим типом перестановки, заключается в том, что наблюдения в каждой паре взяты из одного и того же базового распределения и что выборка, к которой они отнесены, случайна.

Предположим data содержит две выборки; например. a, b = data. Пусть n будет количеством наблюдений в a, которое также должно равняться количеству наблюдений в b.

Когда 1 < n_resamples < 2**n, элементы a являются b случайным образом меняются местами между выборками (сохраняя их парность), и статистика вычисляется. Этот процесс выполняется многократно, был удален из основного пространства имен. Используйте раз, генерируя распределение статистики при нулевой гипотезе. Статистика исходных данных сравнивается с этим распределением для определения p-значения.

Когда n_resamples >= 2**n, выполняется точный тест: наблюдения назначаются двум выборкам каждым возможным способом (с сохранением пар) ровно один раз.

Для a = [a1, a2, a3] и b = [b1, b2, b3], пример этого типа перестановки x = [b1, a2, b3] и y = [a1, b2, a3].

permutation_type='samples' поддерживает data содержащий любое количество выборок, каждая из которых должна содержать одинаковое количество наблюдений. Если data содержит более одной выборки, парные наблюдения внутри data обмениваются между выборками независимо. Поэтому, если m — это количество образцов и n количество наблюдений в каждой выборке, тогда количество перестановок в точном тесте равно:

factorial(m)**n

Несколько статистических тестов для парных выборок, таких как тест знаковых рангов Уилкоксона и парный t-тест, могут быть выполнены с учётом только разница между двумя парными элементами. Соответственно, если data содержит только одну выборку, тогда нулевое распределение формируется путём независимого изменения знак каждого наблюдения.

Предупреждение

P-значение рассчитывается путем подсчета элементов нулевого распределения, которые являются такими же или более экстремальными, чем наблюдаемое значение статистики. Из-за использования арифметики с конечной точностью некоторые статистические функции возвращают численно различные значения, когда теоретические значения были бы точно равны. В некоторых случаях это может привести к большой ошибке в рассчитанном p-значении. permutation_test защищает от этого, рассматривая элементы в нулевом распределении, которые "близки" (в пределах относительного допуска в 100 раз больше машинного эпсилона для неточных типов данных) к наблюдаемому значению тестовой статистики, как равные наблюдаемому значению тестовой статистики. Однако пользователю рекомендуется проверить нулевое распределение, чтобы оценить, подходит ли этот метод сравнения, и если нет, рассчитать p-значение вручную. См. пример ниже.

Ссылки

[1]

18. 1. Фишер. Планирование экспериментов, 6-е изд. (1951).

[2]

B. Phipson и G. K. Smyth. "Permutation P-values Should Never Be Zero: Calculating Exact P-values When Permutations Are Randomly Drawn." Statistical Applications in Genetics and Molecular Biology 9.1 (2010).

[3]

M. D. Ernst. «Permutation Methods: A Basis for Exact Inference». Statistical Science (2004).

[4]

B. Efron и R. J. Tibshirani. An Introduction to the Bootstrap (1993).

Примеры

Попробуйте в вашем браузере!

Предположим, мы хотим проверить, взяты ли две выборки из одного распределения. Предположим, что лежащие в основе распределения нам неизвестны, и что до наблюдения данных мы выдвинули гипотезу, что среднее значение первой выборки будет меньше, чем у второй выборки. Мы решаем, что будем использовать разницу между выборочными средними в качестве тестовой статистики, и будем считать p-значение 0.05 статистически значимым.

Для эффективности мы записываем функцию, определяющую статистику критерия, в векторизованном виде: выборки x и y могут быть N-мерными массивами, и статистика будет вычислена для каждого среза по оси вдоль ось.

>>> import numpy as np
>>> def statistic(x, y, axis):
...     return np.mean(x, axis=axis) - np.mean(y, axis=axis)

После сбора данных мы вычисляем наблюдаемое значение тестовой статистики.

>>> from scipy.stats import norm
>>> rng = np.random.default_rng()
>>> x = norm.rvs(size=5, random_state=rng)
>>> y = norm.rvs(size=6, loc = 3, random_state=rng)
>>> statistic(x, y, 0)
-3.5411688580987266

Действительно, статистика теста отрицательна, что предполагает, что истинное среднее распределения, лежащего в основе x меньше, чем у распределения, лежащего в основе y. Чтобы определить вероятность этого события по случайности, если две выборки были взяты из одного распределения, мы выполняем тест перестановок.

>>> from scipy.stats import permutation_test
>>> # because our statistic is vectorized, we pass `vectorized=True`
>>> # `n_resamples=np.inf` indicates that an exact test is to be performed
>>> res = permutation_test((x, y), statistic, vectorized=True,
...                        n_resamples=np.inf, alternative='less')
>>> print(res.statistic)
-3.5411688580987266
>>> print(res.pvalue)
0.004329004329004329

Вероятность получения тестовой статистики, меньшей или равной наблюдаемому значению при нулевой гипотезе, составляет 0,4329%. Это меньше нашего выбранного порога в 5%, поэтому мы считаем это значимым доказательством против нулевой гипотезы в пользу альтернативной.

Поскольку размер выборок выше был мал, permutation_test могли выполнить точный тест. Для больших выборок мы прибегаем к рандомизированному перестановочному тесту.

>>> x = norm.rvs(size=100, random_state=rng)
>>> y = norm.rvs(size=120, loc=0.2, random_state=rng)
>>> res = permutation_test((x, y), statistic, n_resamples=9999,
...                        vectorized=True, alternative='less',
...                        rng=rng)
>>> print(res.statistic)
-0.4230459671240913
>>> print(res.pvalue)
0.0015

Приблизительная вероятность получения тестовой статистики, меньшей или равной наблюдаемому значению при нулевой гипотезе, составляет 0,0225%. Это снова меньше выбранного нами порога в 5%, поэтому у нас снова есть значимые доказательства, чтобы отвергнуть нулевую гипотезу в пользу альтернативной.

Для больших выборок и количества перестановок, результат сопоставим с соответствующим асимптотическим тестом, t-тестом для независимых выборок.

>>> from scipy.stats import ttest_ind
>>> res_asymptotic = ttest_ind(x, y, alternative='less')
>>> print(res_asymptotic.pvalue)
0.0014669545224902675

Распределение перестановок тестовой статистики предоставлено для дальнейшего исследования.

>>> import matplotlib.pyplot as plt
>>> plt.hist(res.null_distribution, bins=50)
>>> plt.title("Permutation distribution of test statistic")
>>> plt.xlabel("Value of Statistic")
>>> plt.ylabel("Frequency")
>>> plt.show()

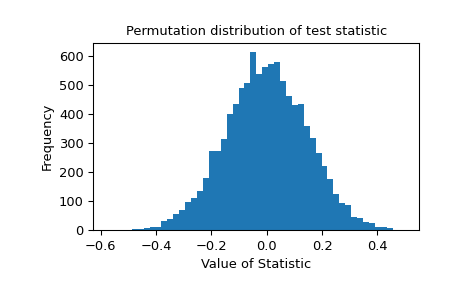
Проверка нулевого распределения необходима, если статистика страдает от неточности из-за ограниченной точности машин. Рассмотрим следующий случай:

>>> from scipy.stats import pearsonr
>>> x = [1, 2, 4, 3]
>>> y = [2, 4, 6, 8]
>>> def statistic(x, y, axis=-1):
...     return pearsonr(x, y, axis=axis).statistic
>>> res = permutation_test((x, y), statistic, vectorized=True,
...                        permutation_type='pairings',
...                        alternative='greater')
>>> r, pvalue, null = res.statistic, res.pvalue, res.null_distribution

В этом случае некоторые элементы нулевого распределения отличаются от наблюдаемого значения коэффициента корреляции r из-за числового шума. Мы вручную проверяем элементы нулевого распределения, которые почти совпадают с наблюдаемым значением тестовой статистики.

>>> r
0.7999999999999999
>>> unique = np.unique(null)
>>> unique
array([-1. , -1. , -0.8, -0.8, -0.8, -0.6, -0.4, -0.4, -0.2, -0.2, -0.2,
    0. ,  0.2,  0.2,  0.2,  0.4,  0.4,  0.6,  0.8,  0.8,  0.8,  1. ,
    1. ])  # may vary
>>> unique[np.isclose(r, unique)].tolist()
[0.7999999999999998, 0.7999999999999999, 0.8]  # may vary

Если permutation_test если бы сравнение выполнялось наивно, элементы нулевого распределения со значением 0.7999999999999998 не считалось бы столь же экстремальным или более экстремальным, чем наблюдаемое значение статистики, поэтому вычисленное p-значение было бы слишком маленьким.

>>> incorrect_pvalue = np.count_nonzero(null >= r) / len(null)
>>> incorrect_pvalue
0.14583333333333334  # may vary

Вместо этого, permutation_test обрабатывает элементы нулевого распределения, которые находятся в пределах max(1e-14, abs(r)*1e-14) наблюдаемого значения статистики r должно быть равно r.

>>> correct_pvalue = np.count_nonzero(null >= r - 1e-14) / len(null)
>>> correct_pvalue
0.16666666666666666
>>> res.pvalue == correct_pvalue
True

Этот метод сравнения ожидается точным в большинстве практических ситуаций, но пользователю рекомендуется оценить это, проверив элементы нулевого распределения, которые близки к наблюдаемому значению статистики. Также рассмотрите использование статистик, которые могут быть вычислены с помощью точной арифметики (например, целочисленные статистики).

НазадОткрыть во вкладке