scipy.stats.qmc.

PoissonDisk#

класс scipy.stats.qmc.PoissonDisk(d, *, radius=0.05, гиперсфера='volume', ncandidates=30, оптимизация=None, rng=None, l_bounds=None, u_bounds=None, seed=None)[источник]#

Дискретизация Пуассона.

Параметры:

dint

Размерность пространства параметров.

radiusfloat

Минимальное расстояние для сохранения между точками при выборке новых кандидатов.

гиперсфера{“volume”, “surface”}, опционально

Стратегия выборки для генерации потенциальных кандидатов, которые могут быть добавлены в окончательную выборку. По умолчанию — 'volume'.

volume: оригинальный алгоритм Бридсона, описанный в [1]. Новые кандидаты выбираются внутри гиперсферу.
surface: только выборка поверхности гиперсферы.

ncandidatesint

Количество кандидатов для выборки на итерацию. Больше кандидатов приводит к более плотной выборке, так как больше кандидатов может быть принято за итерацию.

оптимизация{None, "random-cd", "lloyd"}, опционально

Использовать ли схему оптимизации для улучшения качества после выборки. Обратите внимание, что это постобработка, которая не гарантирует сохранение всех свойств выборки. По умолчанию None.

random-cd: случайные перестановки координат для уменьшения центрированной несоответствия. Лучшая выборка на основе центрированной несоответствия постоянно обновляется. Выборка на основе центрированной несоответствия демонстрирует лучшую устойчивость заполнения пространства для 2D и 3D подпроекций по сравнению с использованием других мер несоответствия.
lloyd: Возмущение выборок с использованием модифицированного алгоритма Ллойда-Макса. Процесс сходится к равноотстоящим выборкам.

Добавлено в версии 1.10.0.

rngnumpy.random.Generator, опционально

Состояние генератора псевдослучайных чисел. Когда rng равно None, новый numpy.random.Generator создаётся с использованием энтропии из операционной системы. Типы, отличные от numpy.random.Generator передаются в numpy.random.default_rng для создания экземпляра Generator.

Изменено в версии 1.15.0: В рамках SPEC-007 переход от использования numpy.random.RandomState to numpy.random.Generator, этот ключевое слово было изменено с seed to rng. В течение переходного периода оба ключевых слова будут продолжать работать, хотя можно указать только одно за раз. После переходного периода вызовы функций с использованием seed ключевое слово будет выдавать предупреждения. После периода устаревания, seed ключевое слово будет удалено.

l_bounds, u_boundsarray_like (d,)

Нижняя и верхняя границы целевых выборочных данных.

Методы

`fast_forward`(n)	Быстрая перемотка последовательности на n позиции.
`fill_space`()	Генерировать `n` выборки в интервале `[l_bounds, u_bounds]`.
`integers`(l_bounds, *[, u_bounds, n, ...])	Генерировать n целые числа от l_bounds (включительно) до u_bounds (исключительно), или если endpoint=True, l_bounds (включительно) до u_bounds (включительно).
`random`([n, workers])	Генерировать n в полуоткрытом интервале `[0, 1)`.
`reset`()	Сбросить движок в базовое состояние.

Примечания

Дискретизация Пуассона — это итеративная стратегия выборки. Начиная с начальной точки выборки, ncandidates выбираются в гиперсфере вокруг начальной точки. Кандидаты ниже определённого radius или вне области определения отклоняются. Новые выборки добавляются в пул начальных значений выборки. Процесс останавливается, когда пул пуст или когда достигнуто требуемое количество выборок.

Максимальное количество точек, которое может содержать выборка, напрямую связано с radius. По мере увеличения размерности пространства, больший радиус распределяет точки дальше и помогает преодолеть проклятие размерности. См. руководство по квази Монте-Карло для получения дополнительной информации.

Предупреждение

Алгоритм более подходит для низких размерностей и размера выборки из-за его итеративной природы и требований к памяти. Выбор малого радиуса при высокой размерности будет означать, что пространство может содержать больше выборок, чем при меньшей размерности или большем радиусе.

Часть кода взята из [2], письменное согласие дано 31.03.2021 оригинальным автором, Shamis, для свободного использования в SciPy под 3-пунктной BSD.

Ссылки

[1]

Robert Bridson, “Fast Poisson Disk Sampling in Arbitrary Dimensions.” SIGGRAPH, 2007.

[2]

StackOverflow.

Примеры

Сгенерировать 2D выборку, используя radius из 0.2.

>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> from matplotlib.collections import PatchCollection
>>> from scipy.stats import qmc
>>>
>>> rng = np.random.default_rng()
>>> radius = 0.2
>>> engine = qmc.PoissonDisk(d=2, radius=radius, rng=rng)
>>> sample = engine.random(20)

Визуализация 2D выборки и демонстрация того, что никакие точки не находятся ближе, чем radius. radius/2 используется для визуализации непересекающихся кругов. Если две выборки находятся точно на radius друг от друга, тогда их окружность радиуса radius/2 коснётся.

>>> fig, ax = plt.subplots()
>>> _ = ax.scatter(sample[:, 0], sample[:, 1])
>>> circles = [plt.Circle((xi, yi), radius=radius/2, fill=False)
...            for xi, yi in sample]
>>> collection = PatchCollection(circles, match_original=True)
>>> ax.add_collection(collection)
>>> _ = ax.set(aspect='equal', xlabel=r'$x_1$', ylabel=r'$x_2$',
...            xlim=[0, 1], ylim=[0, 1])
>>> plt.show()

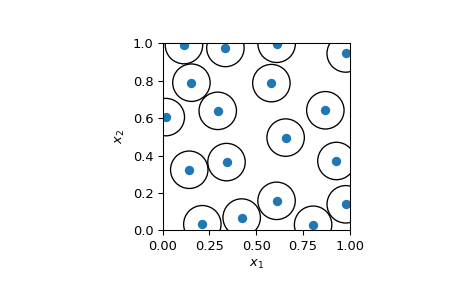
../../_images/scipy-stats-qmc-PoissonDisk-1_00_00.png

Такая визуализация может рассматриваться как упаковка кругов: сколько кругов можно разместить в пространстве. Это NP-трудная задача. Метод fill_space может использоваться для добавления выборок до тех пор, пока больше нельзя будет добавить выборки. Это сложная задача, и параметры, возможно, потребуется настраивать вручную. Остерегайтесь размерности: с увеличением размерности количество выборок, необходимых для заполнения пространства, растёт экспоненциально (проклятие размерности).