Квази-Монте-Карло#

Прежде чем говорить о квази-Монте-Карло (QMC), краткое введение о Монте-Карло (MC). Методы MC, или эксперименты MC, представляют собой широкий класс вычислительных алгоритмов, которые полагаются на повторяющуюся случайную выборку для получения численных результатов. Основная концепция заключается в использовании случайности для решения проблем, которые в принципе могут быть детерминированными. Они часто используются в физических и математических задачах и наиболее полезны, когда сложно или невозможно использовать другие подходы. Методы MC в основном применяются в трех классах задач: оптимизация, численное интегрирование и генерация выборок из распределения вероятностей.

Генерация случайных чисел с определёнными свойствами — более сложная задача, чем кажется. Простые методы Монте-Карло предназначены для выборки точек, которые являются независимыми и одинаково распределёнными (IID). Но генерация нескольких наборов случайных точек может давать радикально разные результаты.

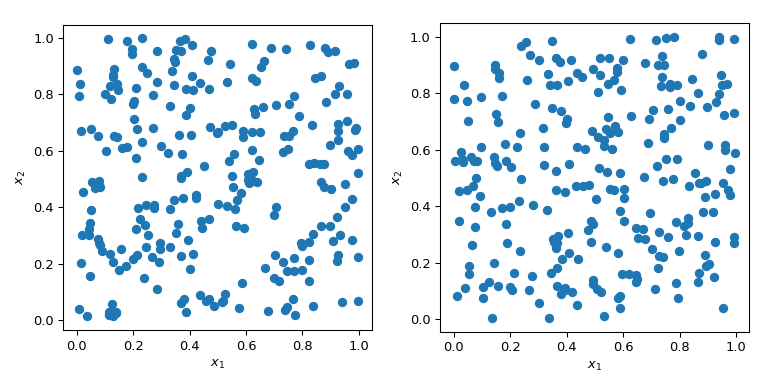
В обоих случаях на графике выше точки генерируются случайным образом без какого-либо знания о ранее нарисованных точках. Ясно, что некоторые области пространства остаются неисследованными - что может вызвать проблемы в симуляциях, так как определенный набор точек может вызвать совершенно другое поведение.

Большое преимущество MC заключается в том, что у него известны свойства сходимости. Давайте посмотрим на среднее квадратичной суммы в 5 измерениях:

\[f(\mathbf{x}) = \left( \sum_{j=1}^{5}x_j \right)^2,\]

с \(x_j \sim \mathcal{U}(0,1)\). Он имеет известное среднее значение, \(\mu = 5/3+5(5-1)/4\). Используя MC-выборку, мы можем численно вычислить это среднее значение, и ошибка аппроксимации следует теоретической скорости \(O(n^{-1/2})\).

Хотя сходимость гарантирована, практики обычно хотят иметь более детерминированный процесс исследования. При обычном Монте-Карло можно использовать seed для повторяемости процесса. Но фиксация seed нарушит свойство сходимости: заданный seed может работать для одного класса задач и не работать для другого.

Что обычно делается для детерминированного обхода пространства — это использование регулярной сетки, охватывающей все размерности параметров, также называемой насыщенным планом. Рассмотрим единичный гиперкуб со всеми границами от 0 до 1. Теперь, при расстоянии 0.1 между точками, количество точек, необходимых для заполнения единичного интервала, составит 10. В двумерном гиперкубе тот же интервал потребует 100, а в трёх измерениях — 1000 точек. По мере роста количества измерений число экспериментов, необходимых для заполнения пространства, растёт экспоненциально с увеличением размерности пространства. Этот экспоненциальный рост называется «проклятием размерности».

>>> import numpy as np
>>> disc = 10
>>> x1 = np.linspace(0, 1, disc)
>>> x2 = np.linspace(0, 1, disc)
>>> x3 = np.linspace(0, 1, disc)
>>> x1, x2, x3 = np.meshgrid(x1, x2, x3)

Для смягчения этой проблемы были разработаны методы QMC. Они являются детерминированными, обеспечивают хорошее покрытие пространства, и некоторые из них могут быть продолжены с сохранением хороших свойств. Основное отличие от методов MC заключается в том, что точки не являются независимыми и одинаково распределенными (IID), а учитывают предыдущие точки. Поэтому некоторые методы также называются последовательностями.

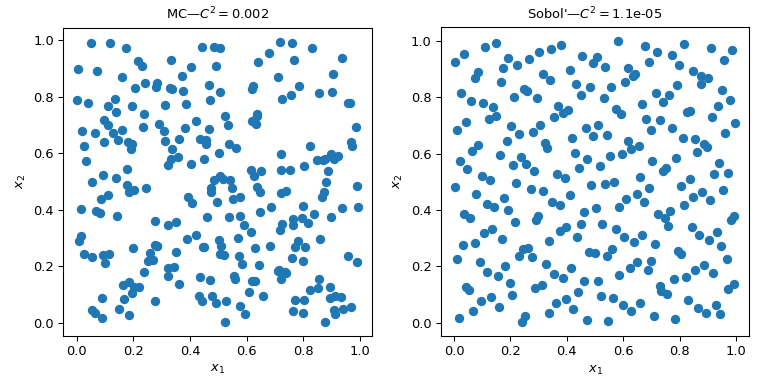
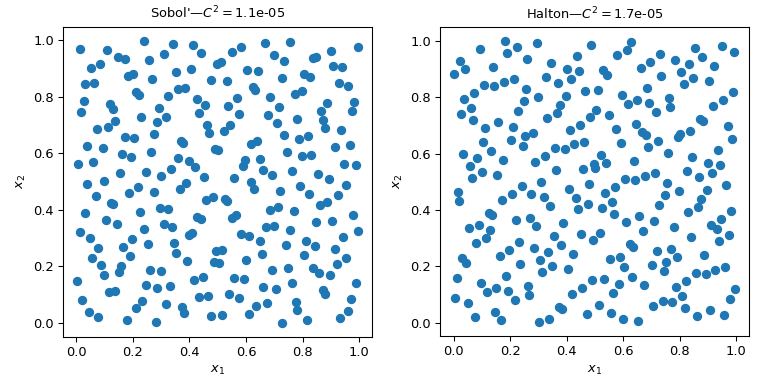
На этом рисунке представлены 2 набора по 256 точек. Дизайн слева — простой метод Монте-Карло, тогда как дизайн справа — QMC-дизайн с использованием Соболя метод. Мы явно видим, что версия QMC более равномерна. Точки лучше распределены вблизи границ, и наблюдается меньше кластеров или пробелов.

Один из способов оценить равномерность — использовать меру, называемую несоответствием. Здесь несоответствие Соболя точек лучше, чем грубый MC.

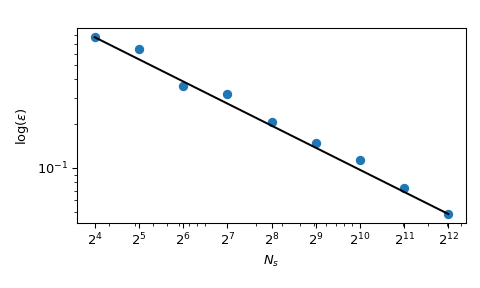
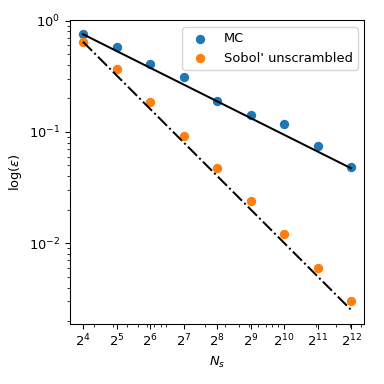
Возвращаясь к вычислению среднего, методы QMC также имеют лучшие скорости сходимости для ошибки. Они могут достигать \(O(n^{-1})\) для этой функции, и даже лучшие скорости на очень гладких функциях. Этот рисунок показывает, что Соболя метод имеет скорость \(O(n^{-1})\):

Мы ссылаемся на документацию scipy.stats.qmc для получения дополнительных математических подробностей.

Вычислить несоответствие#

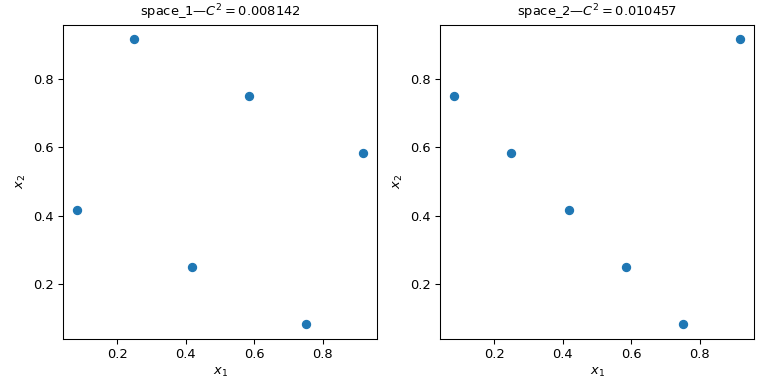
Рассмотрим два набора точек. Из рисунка ниже видно, что конструкция слева покрывает больше пространства, чем конструкция справа. Это можно количественно оценить с помощью scipy.stats.qmc.discrepancy мера. Чем меньше несоответствие, тем более равномерна выборка.

>>> import numpy as np
>>> from scipy.stats import qmc
>>> space_1 = np.array([[1, 3], [2, 6], [3, 2], [4, 5], [5, 1], [6, 4]])
>>> space_2 = np.array([[1, 5], [2, 4], [3, 3], [4, 2], [5, 1], [6, 6]])
>>> l_bounds = [0.5, 0.5]
>>> u_bounds = [6.5, 6.5]
>>> space_1 = qmc.scale(space_1, l_bounds, u_bounds, reverse=True)
>>> space_2 = qmc.scale(space_2, l_bounds, u_bounds, reverse=True)
>>> qmc.discrepancy(space_1)
0.008142039609053464
>>> qmc.discrepancy(space_2)
0.010456854423869011

Использование QMC движка#

Реализовано несколько сэмплеров/движков QMC. Здесь мы рассмотрим два наиболее используемых метода QMC: scipy.stats.qmc.Sobol и scipy.stats.qmc.Halton последовательности.

"""Sobol' and Halton sequences."""
from scipy.stats import qmc
import numpy as np

import matplotlib.pyplot as plt


rng = np.random.default_rng()

n_sample = 256
dim = 2

sample = {}

# Sobol'
engine = qmc.Sobol(d=dim, seed=rng)
sample["Sobol'"] = engine.random(n_sample)

# Halton
engine = qmc.Halton(d=dim, seed=rng)
sample["Halton"] = engine.random(n_sample)

fig, axs = plt.subplots(1, 2, figsize=(8, 4))

for i, kind in enumerate(sample):
    axs[i].scatter(sample[kind][:, 0], sample[kind][:, 1])

    axs[i].set_aspect('equal')
    axs[i].set_xlabel(r'$x_1$')
    axs[i].set_ylabel(r'$x_2$')
    axs[i].set_title(f'{kind}—$C^2 = ${qmc.discrepancy(sample[kind]):.2}')

plt.tight_layout()
plt.show()

Предупреждение

Методы QMC требуют особой осторожности, и пользователь должен прочитать документацию, чтобы избежать распространённых ошибок. Соболя например, требует количество точек, следующее за степенью 2. Также, прореживание, сжигание или другой выбор точек может нарушить свойства последовательности и привести к набору точек, который не будет лучше, чем MC.

QMC движки учитывают состояние. Это означает, что вы можете продолжить последовательность, пропустить некоторые точки или сбросить её. Возьмём 5 точек из scipy.stats.qmc.Halton. А затем запросить второй набор из 5 точек:

>>> from scipy.stats import qmc
>>> engine = qmc.Halton(d=2)
>>> engine.random(5)
array([[0.22166437, 0.07980522],  # random
       [0.72166437, 0.93165708],
       [0.47166437, 0.41313856],
       [0.97166437, 0.19091633],
       [0.01853937, 0.74647189]])
>>> engine.random(5)
array([[0.51853937, 0.52424967],  # random
       [0.26853937, 0.30202745],
       [0.76853937, 0.857583  ],
       [0.14353937, 0.63536078],
       [0.64353937, 0.01807683]])

Теперь мы сбрасываем последовательность. Запрос 5 точек приводит к тем же первым 5 точкам:

>>> engine.reset()
>>> engine.random(5)
array([[0.22166437, 0.07980522],  # random
       [0.72166437, 0.93165708],
       [0.47166437, 0.41313856],
       [0.97166437, 0.19091633],
       [0.01853937, 0.74647189]])

И здесь мы продвигаем последовательность, чтобы получить тот же второй набор из 5 точек:

>>> engine.reset()
>>> engine.fast_forward(5)
>>> engine.random(5)
array([[0.51853937, 0.52424967],  # random
       [0.26853937, 0.30202745],
       [0.76853937, 0.857583  ],
       [0.14353937, 0.63536078],
       [0.64353937, 0.01807683]])

Примечание

По умолчанию, оба scipy.stats.qmc.Sobol и scipy.stats.qmc.Halton перемешаны. Свойства сходимости лучше, и это предотвращает появление полос или заметных узоров точек в высоких размерностях. Нет практических причин не использовать перемешанную версию.

Создание движка QMC, т.е. создание подкласса `QMCEngine`#

Чтобы создать свой собственный scipy.stats.qmc.QMCEngine, несколько методов должны быть определены. Ниже приведен пример обёртки numpy.random.Generator.

>>> import numpy as np
>>> from scipy.stats import qmc
>>> class RandomEngine(qmc.QMCEngine):
...     def __init__(self, d, seed=None):
...         super().__init__(d=d, seed=seed)
...         self.rng = np.random.default_rng(self.rng_seed)
...
...
...     def _random(self, n=1, *, workers=1):
...         return self.rng.random((n, self.d))
...
...
...     def reset(self):
...         self.rng = np.random.default_rng(self.rng_seed)
...         self.num_generated = 0
...         return self
...
...
...     def fast_forward(self, n):
...         self.random(n)
...         return self

Затем мы используем его как любой другой QMC-движок:

>>> engine = RandomEngine(2)
>>> engine.random(5)
array([[0.22733602, 0.31675834],  # random
       [0.79736546, 0.67625467],
       [0.39110955, 0.33281393],
       [0.59830875, 0.18673419],
       [0.67275604, 0.94180287]])
>>> engine.reset()
>>> engine.random(5)
array([[0.22733602, 0.31675834],  # random
       [0.79736546, 0.67625467],
       [0.39110955, 0.33281393],
       [0.59830875, 0.18673419],
       [0.67275604, 0.94180287]])

Квази-Монте-Карло#

Вычислить несоответствие#

Использование QMC движка#

Создание движка QMC, т.е. создание подкласса QMCEngine#

Рекомендации по использованию QMC#

Создание движка QMC, т.е. создание подкласса `QMCEngine`#