scipy.stats.qmc.

geometric_discrepancy

scipy.stats.qmc.geometric_discrepancy(sample, метод='mindist', метрика='euclidean')

Несогласованность заданной выборки на основе её геометрических свойств.

Параметры:

samplearray_like (n, d)

Образец, от которого вычисляется расхождение.

метод{“mindist”, “mst”}, опционально

Метод для использования. Один из mindist для минимального расстояния (по умолчанию) или mst для минимального остовного дерева.

метрикаstr или callable, опционально

Метрика расстояния для использования. См. документацию для scipy.spatial.distance.pdist для доступных метрик и значения по умолчанию.

Возвращает:

несоответствиеfloat

Расхождение (большие значения соответствуют большей однородности выборки).

Смотрите также

discrepancy

Примечания

Несоответствие может служить простой мерой качества случайной выборки. Эта мера основана на геометрических свойствах распределения точек в выборке, таких как минимальное расстояние между любой парой точек или средняя длина ребра в минимальном остовном дереве.

Чем выше значение, тем лучше покрытие пространства параметров. Обратите внимание, что это отличается от scipy.stats.qmc.discrepancy, где меньшие значения соответствуют более высокому качеству выборки.

Также обратите внимание, что при сравнении различных стратегий выборки с использованием этой функции размер выборки должен оставаться постоянным.

Возможно вычислить две метрики из минимального остовного дерева: среднюю длину ребра и стандартное отклонение длин ребер. Использование обеих метрик дает лучшее представление о равномерности, чем каждая метрика по отдельности, причем предпочтительны более высокое среднее значение и меньшее стандартное отклонение (см. [1] для краткого обсуждения). Эта функция в настоящее время вычисляет только среднюю длину ребра.

Ссылки

[1]

Franco J. et al. “Minimum Spanning Tree: A new approach to assess the quality of the design of computer experiments.” Chemometrics and Intelligent Laboratory Systems, 97 (2), pp. 164-169, 2009.

Примеры

Попробуйте в вашем браузере!

Вычисление качества выборки с использованием минимального евклидова расстояния (по умолчанию):

>>> import numpy as np
>>> from scipy.stats import qmc
>>> rng = np.random.default_rng()
>>> sample = qmc.LatinHypercube(d=2, rng=rng).random(50)
>>> qmc.geometric_discrepancy(sample)
0.03708161435687876

Рассчитать качество, используя среднюю длину ребра в минимальном остовном дереве:

>>> qmc.geometric_discrepancy(sample, method='mst')
0.1105149978798376

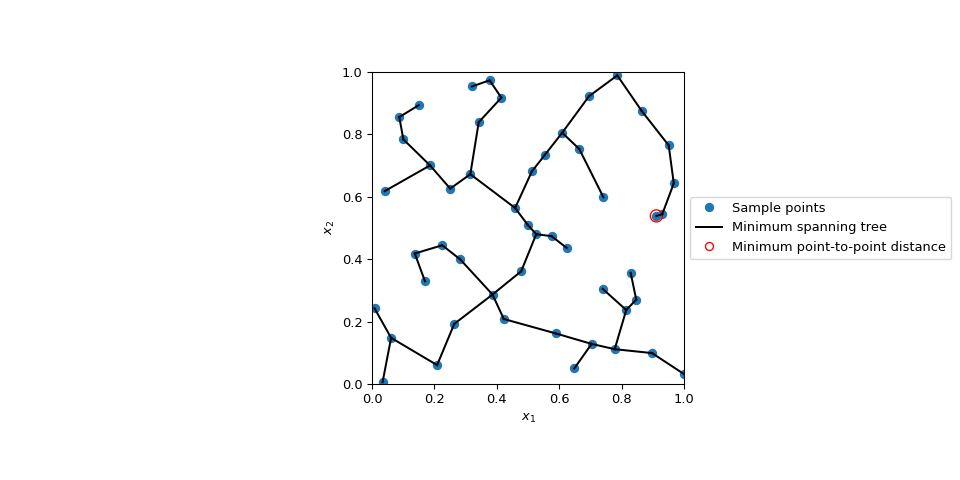
Отобразить минимальное остовное дерево и точки с наименьшим расстоянием:

>>> import matplotlib.pyplot as plt
>>> from matplotlib.lines import Line2D
>>> from scipy.sparse.csgraph import minimum_spanning_tree
>>> from scipy.spatial.distance import pdist, squareform
>>> dist = pdist(sample)
>>> mst = minimum_spanning_tree(squareform(dist))
>>> edges = np.where(mst.toarray() > 0)
>>> edges = np.asarray(edges).T
>>> min_dist = np.min(dist)
>>> min_idx = np.argwhere(squareform(dist) == min_dist)[0]
>>> fig, ax = plt.subplots(figsize=(10, 5))
>>> _ = ax.set(aspect='equal', xlabel=r'$x_1$', ylabel=r'$x_2$',
...            xlim=[0, 1], ylim=[0, 1])
>>> for edge in edges:
...     ax.plot(sample[edge, 0], sample[edge, 1], c='k')
>>> ax.scatter(sample[:, 0], sample[:, 1])
>>> ax.add_patch(plt.Circle(sample[min_idx[0]], min_dist, color='red', fill=False))
>>> markers = [
...     Line2D([0], [0], marker='o', lw=0, label='Sample points'),
...     Line2D([0], [0], color='k', label='Minimum spanning tree'),
...     Line2D([0], [0], marker='o', lw=0, markerfacecolor='w', markeredgecolor='r',
...            label='Minimum point-to-point distance'),
... ]
>>> ax.legend(handles=markers, loc='center left', bbox_to_anchor=(1, 0.5));
>>> plt.show()

НазадОткрыть во вкладке