scipy.stats.sampling.

NumericalInversePolynomial

класс scipy.stats.sampling.NumericalInversePolynomial(dist, *, mode=None, центр=None, область определения=None, порядок=5, u_resolution=1e-10, random_state=None)

Полиномиальная интерполяция на основе инверсии CDF (PINV).

PINV — это вариант численной инверсии, где обратная CDF аппроксимируется с использованием интерполяционной формулы Ньютона. Интервал [0,1] разбивается на несколько подынтервалов. В каждом из них обратная CDF строится в узлах (CDF(x),x) для некоторых точек x в этом подынтервале. Если задана PDF, то CDF вычисляется численно из заданной PDF с использованием адаптивного интегрирования Гаусса-Лобатто с 5 точками. Подынтервалы разделяются до достижения требуемой точности.

Метод не является точным, так как он производит только случайные величины аппроксимированного распределения. Тем не менее, максимально допустимая ошибка аппроксимации может быть установлена равной разрешению (но, конечно, ограничена машинной точностью). Мы используем u-ошибку |U - CDF(X)| для измерения ошибки, где X является приблизительным процентилем, соответствующим квантилю U т.е. X = approx_ppf(U). Мы называем максимально допустимую u-ошибку u-разрешением алгоритма.

Можно выбрать как порядок интерполяционного полинома, так и разрешение по u. Обратите внимание, что возможны очень маленькие значения разрешения по u, но они увеличивают стоимость шага настройки.

Интерполирующие полиномы должны быть вычислены на этапе настройки. Однако это работает только для распределений с ограниченной областью; для распределений с неограниченной областью хвосты обрезаются так, что вероятность для хвостовых областей мала по сравнению с заданным u-разрешением.

Построение интерполяционного полинома работает только тогда, когда PDF унимодален или когда PDF не обращается в ноль между двумя модами.

Существуют некоторые ограничения для данного распределения:

• Носитель распределения (т.е. область, где PDF строго положителен) должен быть связным. На практике это означает, что область, где PDF "не слишком мал", должна быть связной. Унимодальные плотности удовлетворяют этому условию. Если это условие нарушено, то область определения распределения может быть усечена.

• Когда PDF интегрируется численно, то заданный PDF должен быть непрерывным и должен быть гладким.

• PDF должен быть ограниченным.

• Алгоритм имеет проблемы, когда распределение имеет тяжёлые хвосты (тогда обратная CDF становится очень крутой при 0 или 1) и запрошенное u-разрешение очень мало. Например, распределение Коши, вероятно, покажет эту проблему, когда запрошенное u-разрешение меньше 1.e-12.

Параметры:

distobject

Экземпляр класса с pdf или logpdf method, опционально cdf метод.

• pdf: PDF распределения. Ожидается, что сигнатура PDF будет: def pdf(self, x: float) -> float, т.е., PDF должен принимать Python float и возвращать Python float. Ему не нужно интегрироваться в 1, т.е., PDF не нужно нормализовать. Этот метод опционален, но либо pdf или logpdf должны быть указаны. Если оба даны, logpdf используется.

• logpdf: Логарифм PDF распределения. Сигнатура такая же, как у pdf. Аналогично, логарифм нормировочной константы ПРВ можно игнорировать. Этот метод является необязательным, но либо pdf или logpdf должны быть указаны. Если оба даны, logpdf используется.

• cdf: CDF распределения. Этот метод опционален. Если предоставлен, он позволяет вычислять "u-ошибку". См. u_error. Должен иметь ту же сигнатуру, что и PDF.

modefloat, опционально

(Точная) Мода распределения. По умолчанию None.

центрfloat, опционально

Приблизительное расположение моды или среднего распределения. Это расположение даёт некоторую информацию об основной части PDF и используется для избежания численных проблем. По умолчанию None.

область определениясписок или кортеж длины 2, опционально

Носитель распределения. По умолчанию None. Когда None:

• Если support метод предоставляется объектом распределения dist, используется для установки области определения распределения.

• В противном случае предполагается, что носитель \((-\infty, \infty)\).

порядокint, необязательный

Порядок интерполирующего полинома. Допустимые порядки от 3 до 17. Более высокие порядки приводят к меньшему количеству интервалов для аппроксимаций. По умолчанию 5.

u_resolutionfloat, опционально

Установить максимально допустимую u-ошибку. Значения u_resolution должны быть не менее 1.e-15 и не более 1.e-5. Заметим, что разрешение большинства источников равномерных случайных чисел составляет 2-32= 2.3e-10. Таким образом, значение 1.e-10 приводит к алгоритму инверсии, который можно назвать точным. Для большинства симуляций достаточно и немного больших значений для максимальной ошибки. По умолчанию 1e-10.

random_state{None, int, numpy.random.Generator,

numpy.random.RandomState, опционально

Генератор случайных чисел NumPy или seed для базового генератора случайных чисел NumPy, используемого для генерации потока равномерных случайных чисел. Если random_state равно None (или np.random), numpy.random.RandomState используется синглтон. Если random_state является int, новый RandomState используется экземпляр, инициализированный с random_state. Если random_state уже является Generator или RandomState экземпляр, тогда этот экземпляр используется.

Атрибуты:

intervals

Получить количество интервалов, используемых в вычислениях.

Методы

cdf(x)	Аппроксимированная кумулятивная функция распределения заданного распределения.
ppf(u)	Приближенная PPF заданного распределения.
qrvs([size, d, qmc_engine])	Квазислучайные величины заданной случайной величины.
rvs([size, random_state])	Выборка из распределения.
set_random_state([random_state])	Установить базовый генератор равномерных случайных чисел.
u_error([sample_size])	Оценить u-ошибку аппроксимации с помощью метода Монте-Карло.

Ссылки

[1]

Дерфлингер, Герхард, Вольфганг Хёрманн и Йозеф Лейдольд. «Генерация случайных величин путем численной инверсии, когда известна только плотность». ACM Transactions on Modeling and Computer Simulation (TOMACS) 20.4 (2010): 1-25.

[2]

Справочное руководство UNU.RAN, Раздел 5.3.12, «PINV - Инверсия CDF на основе полиномиальной интерполяции», https://statmath.wu.ac.at/software/unuran/doc/unuran.html#PINV

Примеры

Попробуйте в вашем браузере!

>>> from scipy.stats.sampling import NumericalInversePolynomial
>>> from scipy.stats import norm
>>> import numpy as np

Чтобы создать генератор для выборки из стандартного нормального распределения, сделайте:

>>> class StandardNormal:
...    def pdf(self, x):
...        return np.exp(-0.5 * x*x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInversePolynomial(dist, random_state=urng)

После создания генератора, выборки могут быть извлечены из распределения путем вызова rvs method:

>>> rng.rvs()
-1.5244996276336318

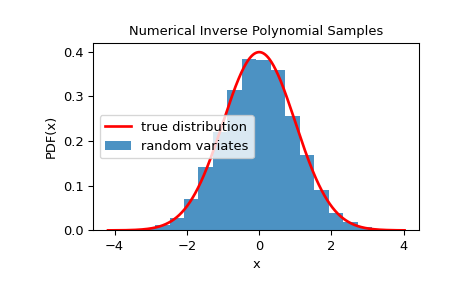
Чтобы проверить, что случайные величины близко следуют заданному распределению, мы можем посмотреть на его гистограмму:

>>> import matplotlib.pyplot as plt
>>> rvs = rng.rvs(10000)
>>> x = np.linspace(rvs.min()-0.1, rvs.max()+0.1, 1000)
>>> fx = norm.pdf(x)
>>> plt.plot(x, fx, 'r-', lw=2, label='true distribution')
>>> plt.hist(rvs, bins=20, density=True, alpha=0.8, label='random variates')
>>> plt.xlabel('x')
>>> plt.ylabel('PDF(x)')
>>> plt.title('Numerical Inverse Polynomial Samples')
>>> plt.legend()
>>> plt.show()

Можно оценить u-ошибку приближенной PPF, если точная CDF доступна во время настройки. Для этого передайте dist объект с точной CDF распределения во время инициализации:

>>> from scipy.special import ndtr
>>> class StandardNormal:
...    def pdf(self, x):
...        return np.exp(-0.5 * x*x)
...    def cdf(self, x):
...        return ndtr(x)
...
>>> dist = StandardNormal()
>>> urng = np.random.default_rng()
>>> rng = NumericalInversePolynomial(dist, random_state=urng)

Теперь u-ошибка может быть оценена вызовом u_error метод. Он запускает симуляцию Монте-Карло для оценки u-ошибки. По умолчанию используется 100000 выборок. Чтобы изменить это, можно передать количество выборок в качестве аргумента:

>>> rng.u_error(sample_size=1000000)  # uses one million samples
UError(max_error=8.785994154436594e-11, mean_absolute_error=2.930890027826552e-11)

Это возвращает namedtuple, который содержит максимальную u-ошибку и среднюю абсолютную u-ошибку.

U-ошибку можно уменьшить, снизив u-разрешение (максимально допустимая u-ошибка):

>>> urng = np.random.default_rng()
>>> rng = NumericalInversePolynomial(dist, u_resolution=1.e-12, random_state=urng)
>>> rng.u_error(sample_size=1000000)
UError(max_error=9.07496300328603e-13, mean_absolute_error=3.5255644517257716e-13)

Обратите внимание, что это происходит за счёт увеличения времени настройки.

Приближённая PPF может быть вычислена вызовом ppf method:

>>> rng.ppf(0.975)
1.9599639857012559
>>> norm.ppf(0.975)
1.959963984540054

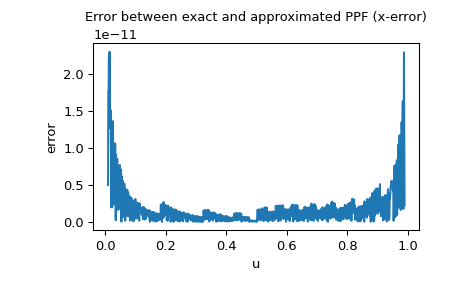
Поскольку PPF нормального распределения доступен как специальная функция, мы также можем проверить x-ошибку, т.е. разницу между аппроксимированным PPF и точным PPF:

>>> import matplotlib.pyplot as plt
>>> u = np.linspace(0.01, 0.99, 1000)
>>> approxppf = rng.ppf(u)
>>> exactppf = norm.ppf(u)
>>> error = np.abs(exactppf - approxppf)
>>> plt.plot(u, error)
>>> plt.xlabel('u')
>>> plt.ylabel('error')
>>> plt.title('Error between exact and approximated PPF (x-error)')
>>> plt.show()

НазадОткрыть во вкладке