индексы Соболя#
- scipy.stats.индексы Соболя(*, функция, n, распределения=None, метод='saltelli_2010', rng=None, random_state=None)[источник]#
Глобальные индексы чувствительности Соболя.
- Параметры:
- функцияcallable или dict(str, array_like)
Если функция является вызываемым объектом, функцией для вычисления индексов Соболя. Его сигнатура должна быть:
func(x: ArrayLike) -> ArrayLike
с
xформы(d, n)и выходной формы(s, n)где:dявляется входной размерностью функция (количество входных переменных),sявляется выходной размерностью функция (количество выходных переменных), иn— это количество образцов (см. n ниже).
Значения оценки функции должны быть конечными.
Если функция является словарём, содержащим вычисления функции из трёх различных массивов. Ключи должны быть:
f_A,f_Bиf_AB.f_Aиf_Bдолжен иметь форму(s, n)иf_ABдолжен иметь форму(d, s, n). Это продвинутая функция, и неправильное использование может привести к ошибочному анализу.- nint
Количество выборок, использованных для генерации матриц
AиB. Должно быть степенью 2. Общее количество точек, в которых функция будет вычисленоn*(d+2).- распределенияlist(distributions), optional
Список распределений каждого параметра. Распределение параметров зависит от приложения и должно быть тщательно выбрано. Предполагается, что параметры распределены независимо, то есть нет ограничений или связей между их значениями.
Распределения должны быть экземпляром класса с
ppfметод.Должен быть указан, если функция является вызываемым объектом, и игнорируется в противном случае.
- методCallable или str, по умолчанию: 'saltelli_2010'
Метод, используемый для вычисления первых и общих индексов Соболя.
Если вызываемый объект, его сигнатура должна быть:
func(f_A: np.ndarray, f_B: np.ndarray, f_AB: np.ndarray) -> Tuple[np.ndarray, np.ndarray]
с
f_A, f_Bформы(s, n)иf_ABформы(d, s, n). Эти массивы содержат вычисления функций из трёх различных наборов выборок. Выходные данные — это кортеж из первого и общего индексов с формой(s, d). Это продвинутая функция, и неправильное использование может привести к ошибочному анализу.- rng
numpy.random.Generator, опционально Состояние генератора псевдослучайных чисел. Когда rng равно None, новый
numpy.random.Generatorсоздаётся с использованием энтропии из операционной системы. Типы, отличные отnumpy.random.Generatorпередаются вnumpy.random.default_rngдля создания экземпляраGenerator.Изменено в версии 1.15.0: В рамках SPEC-007 переход от использования
numpy.random.RandomStatetonumpy.random.Generator, этот ключевое слово было изменено с random_state to rng. В течение переходного периода оба ключевых слова будут продолжать работать, хотя можно указать только одно за раз. После переходного периода вызовы функций с использованием random_state ключевое слово будет выдавать предупреждения. После периода устаревания, random_state ключевое слово будет удалено.
- Возвращает:
- resSobolResult
Объект с атрибутами:
- first_orderndarray формы (s, d)
Индексы Соболя первого порядка.
- total_orderndarray формы (s, d)
Индексы Соболя полного порядка.
И метод:
bootstrap(confidence_level: float, n_resamples: int) -> BootstrapSobolResult
Метод, предоставляющий доверительные интервалы для индексов. См.
scipy.stats.bootstrapдля получения дополнительной информации.Бутстраппинг выполняется как для индексов первого, так и для общего порядка, и они доступны в BootstrapSobolResult как атрибуты
first_orderиtotal_order.
Примечания
Метод Соболя [1], [2] является дисперсионным анализом чувствительности, который получает вклад каждого параметра в дисперсию интересующих величин (QoIs; т.е. выходных данных функция). Соответствующие вклады могут использоваться для ранжирования параметров и также оценки сложности модели путём вычисления эффективной (или средней) размерности модели.
Примечание
Предполагается, что параметры распределены независимо. Каждый параметр всё ещё может следовать любому распределению. На самом деле, распределение очень важно и должно соответствовать реальному распределению параметров.
Использует функциональное разложение дисперсии функции для исследования
\[\mathbb{V}(Y) = \sum_{i}^{d} \mathbb{V}_i (Y) + \sum_{iвведение условных дисперсий:
\[\mathbb{V}_i(Y) = \mathbb{\mathbb{V}}[\mathbb{E}(Y|x_i)] \qquad \mathbb{V}_{ij}(Y) = \mathbb{\mathbb{V}}[\mathbb{E}(Y|x_i x_j)] - \mathbb{V}_i(Y) - \mathbb{V}_j(Y),\]Индексы Соболя выражаются как
\[S_i = \frac{\mathbb{V}_i(Y)}{\mathbb{V}[Y]} \qquad S_{ij} =\frac{\mathbb{V}_{ij}(Y)}{\mathbb{V}[Y]}.\]\(S_{i}\) соответствует члену первого порядка, который учитывает вклад i-го параметра, в то время как \(S_{ij}\) соответствует члену второго порядка, который информирует о вкладе взаимодействий между i-м и j-м параметрами. Эти уравнения могут быть обобщены для вычисления членов более высокого порядка; однако их вычисление дорого, а интерпретация сложна. Поэтому предоставляются только индексы первого порядка.
Индексы полного порядка представляют глобальный вклад параметров в дисперсию QoI и определяются как:
\[S_{T_i} = S_i + \sum_j S_{ij} + \sum_{j,k} S_{ijk} + ... = 1 - \frac{\mathbb{V}[\mathbb{E}(Y|x_{\sim i})]}{\mathbb{V}[Y]}.\]Индексы первого порядка суммируются не более чем до 1, а индексы общего порядка суммируются не менее чем до 1. Если взаимодействий нет, то индексы первого и общего порядка равны, и оба суммируются до 1.
Предупреждение
Отрицательные значения Соболя обусловлены численными ошибками. Увеличение количества точек n должно помочь.
Количество выборок, необходимое для хорошего анализа, увеличивается с размерностью задачи. Например, для 3-мерной задачи рассмотрите как минимум
n >= 2**12. Чем сложнее модель, тем больше выборок потребуется.Даже для чисто аддитивной модели индексы могут не суммироваться до 1 из-за числового шума.
Ссылки
[1]Соболь, И. М.. "Анализ чувствительности для нелинейных математических моделей." Математическое моделирование и вычислительный эксперимент, 1:407-414, 1993.
[2]Соболь, И. М. (2001). "Глобальные индексы чувствительности для нелинейных математических моделей и их оценки методом Монте-Карло." Mathematics and Computers in Simulation, 55(1-3):271-280, DOI:10.1016/S0378-4754(00)00270-6, 2001.
[3]Saltelli, A. “Making best use of model evaluations to compute sensitivity indices.” Computer Physics Communications, 145(2):280-297, DOI:10.1016/S0010-4655(02)00280-1, 2002.
[4]Saltelli, A., M. Ratto, T. Andres, F. Campolongo, J. Cariboni, D. Gatelli, M. Saisana, and S. Tarantola. "Global Sensitivity Analysis. The Primer." 2007.
[5]Saltelli, A., P. Annoni, I. Azzini, F. Campolongo, M. Ratto, и S. Tarantola. «Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index.» Computer Physics Communications, 181(2):259-270, DOI:10.1016/j.cpc.2009.09.018, 2010.
[6]Ишигами, Т. и Т. Хомма. «Техника количественной оценки важности в анализе неопределённости для компьютерных моделей». IEEE, DOI:10.1109/ISUMA.1990.151285, 1990.
Примеры
Ниже приведен пример с функцией Ишигами [6]
\[Y(\mathbf{x}) = \sin x_1 + 7 \sin^2 x_2 + 0.1 x_3^4 \sin x_1,\]с \(\mathbf{x} \in [-\pi, \pi]^3\). Эта функция демонстрирует сильную нелинейность и немонотонность.
Помните, что индексы Соболя предполагают, что выборки распределены независимо. В этом случае мы используем равномерное распределение на каждом маргинале.
>>> import numpy as np >>> from scipy.stats import sobol_indices, uniform >>> rng = np.random.default_rng() >>> def f_ishigami(x): ... f_eval = ( ... np.sin(x[0]) ... + 7 * np.sin(x[1])**2 ... + 0.1 * (x[2]**4) * np.sin(x[0]) ... ) ... return f_eval >>> indices = sobol_indices( ... func=f_ishigami, n=1024, ... dists=[ ... uniform(loc=-np.pi, scale=2*np.pi), ... uniform(loc=-np.pi, scale=2*np.pi), ... uniform(loc=-np.pi, scale=2*np.pi) ... ], ... rng=rng ... ) >>> indices.first_order array([0.31637954, 0.43781162, 0.00318825]) >>> indices.total_order array([0.56122127, 0.44287857, 0.24229595])
Доверительный интервал может быть получен с помощью бутстреппинга.
>>> boot = indices.bootstrap()
Затем эту информацию можно легко визуализировать.
>>> import matplotlib.pyplot as plt >>> fig, axs = plt.subplots(1, 2, figsize=(9, 4)) >>> _ = axs[0].errorbar( ... [1, 2, 3], indices.first_order, fmt='o', ... yerr=[ ... indices.first_order - boot.first_order.confidence_interval.low, ... boot.first_order.confidence_interval.high - indices.first_order ... ], ... ) >>> axs[0].set_ylabel("First order Sobol' indices") >>> axs[0].set_xlabel('Input parameters') >>> axs[0].set_xticks([1, 2, 3]) >>> _ = axs[1].errorbar( ... [1, 2, 3], indices.total_order, fmt='o', ... yerr=[ ... indices.total_order - boot.total_order.confidence_interval.low, ... boot.total_order.confidence_interval.high - indices.total_order ... ], ... ) >>> axs[1].set_ylabel("Total order Sobol' indices") >>> axs[1].set_xlabel('Input parameters') >>> axs[1].set_xticks([1, 2, 3]) >>> plt.tight_layout() >>> plt.show()
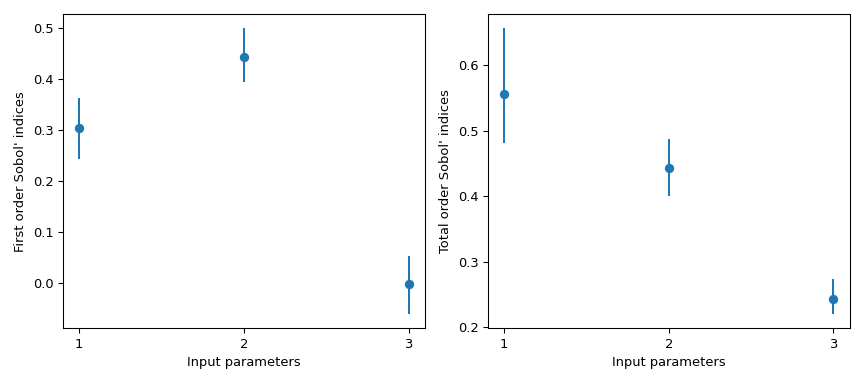
Примечание
По умолчанию,
scipy.stats.uniformимеет носитель[0, 1]. Используя параметрыlocиscale, получается равномерное распределение на[loc, loc + scale].Этот результат особенно интересен, потому что индекс первого порядка \(S_{x_3} = 0\) тогда как его полный порядок равен \(S_{T_{x_3}} = 0.244\)Это означает, что взаимодействия более высокого порядка с \(x_3\) отвечают за разницу. Почти 25% наблюдаемой дисперсии в QoI обусловлено корреляциями между \(x_3\) и \(x_1\), хотя \(x_3\) сам по себе не влияет на QoI.
Следующее дает визуальное объяснение индексов Соболя для этой функции. Сгенерируем 1024 выборки в \([-\pi, \pi]^3\) и вычислить значение выхода.
>>> from scipy.stats import qmc >>> n_dim = 3 >>> p_labels = ['$x_1$', '$x_2$', '$x_3$'] >>> sample = qmc.Sobol(d=n_dim, seed=rng).random(1024) >>> sample = qmc.scale( ... sample=sample, ... l_bounds=[-np.pi, -np.pi, -np.pi], ... u_bounds=[np.pi, np.pi, np.pi] ... ) >>> output = f_ishigami(sample.T)
Теперь мы можем строить диаграммы рассеяния выхода относительно каждого параметра. Это даёт визуальный способ понять, как каждый параметр влияет на выход функции.
>>> fig, ax = plt.subplots(1, n_dim, figsize=(12, 4)) >>> for i in range(n_dim): ... xi = sample[:, i] ... ax[i].scatter(xi, output, marker='+') ... ax[i].set_xlabel(p_labels[i]) >>> ax[0].set_ylabel('Y') >>> plt.tight_layout() >>> plt.show()
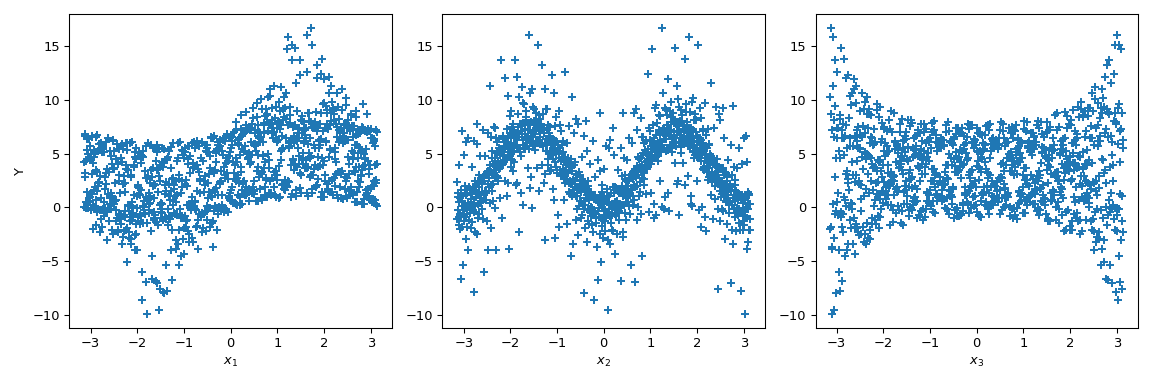
Теперь Sobol’ идет дальше: условливая выходное значение заданными значениями параметра (черные линии), вычисляется условное среднее выходное значение. Это соответствует термину \(\mathbb{E}(Y|x_i)\). Вычисление дисперсии этого члена дает числитель индексов Соболя.
>>> mini = np.min(output) >>> maxi = np.max(output) >>> n_bins = 10 >>> bins = np.linspace(-np.pi, np.pi, num=n_bins, endpoint=False) >>> dx = bins[1] - bins[0] >>> fig, ax = plt.subplots(1, n_dim, figsize=(12, 4)) >>> for i in range(n_dim): ... xi = sample[:, i] ... ax[i].scatter(xi, output, marker='+') ... ax[i].set_xlabel(p_labels[i]) ... for bin_ in bins: ... idx = np.where((bin_ <= xi) & (xi <= bin_ + dx)) ... xi_ = xi[idx] ... y_ = output[idx] ... ave_y_ = np.mean(y_) ... ax[i].plot([bin_ + dx/2] * 2, [mini, maxi], c='k') ... ax[i].scatter(bin_ + dx/2, ave_y_, c='r') >>> ax[0].set_ylabel('Y') >>> plt.tight_layout() >>> plt.show()
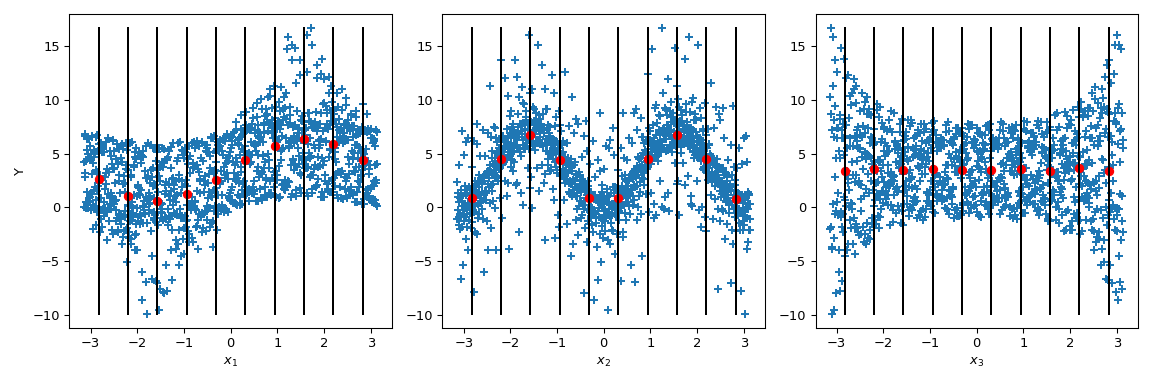
Рассматривая \(x_3\), дисперсия среднего равна нулю, что приводит к \(S_{x_3} = 0\). Но мы можем дополнительно наблюдать, что дисперсия выхода не постоянна вдоль значений параметра \(x_3\). Эта гетероскедастичность объясняется взаимодействиями более высокого порядка. Кроме того, гетероскедастичность также заметна на \(x_1\) приводя к взаимодействию между \(x_3\) и \(x_1\). На \(x_2\), дисперсия, по-видимому, постоянна, и, следовательно, можно предположить нулевое взаимодействие с этим параметром.
Этот случай довольно прост для визуального анализа — хотя это только качественный анализ. Тем не менее, когда количество входных параметров увеличивается, такой анализ становится нереалистичным, так как будет сложно сделать выводы о членах высокого порядка. Отсюда польза использования индексов Соболя.