scipy.stats.

bootstrap

scipy.stats.bootstrap(данные, статистика, *, n_resamples=9999, batch=None, векторизованный=None, paired=False, ось=0, confidence_level=0.95, альтернатива='two-sided', метод='BCa', bootstrap_result=None, rng=None, random_state=None)

Вычислите двусторонний бутстрап-доверительный интервал статистики.

Когда метод является 'percentile' и альтернатива является 'two-sided', доверительный интервал бутстрепа вычисляется согласно следующей процедуре.

1. Передискретизация данных: для каждого образца в данные и для каждого из n_resamples, возьмите случайную выборку из исходной выборки (с возвращением) того же размера, что и исходная выборка.

2. Вычислить бутстрап-распределение статистики: для каждого набора ресемплов вычислить тестовую статистику.

3. Определить доверительный интервал: найти интервал бутстрап- распределения, который

   • симметрично относительно медианы и

   • содержит confidence_level из значений перевыборочной статистики.

Хотя 'percentile' метод является наиболее интуитивным, но на практике он редко используется. Доступны два более распространённых метода: 'basic' (‘обратный процентиль’) и 'BCa' (‘bias-corrected and accelerated’); они отличаются тем, как выполняется шаг 3.

Если выборки в данные берутся случайным образом из соответствующих распределений \(n\) раз, доверительный интервал, возвращаемый bootstrap будет содержать истинное значение статистики для этих распределений приблизительно confidence_level\(\, \times \, n\) раз.

Параметры:

данныепоследовательность array-like

Каждый элемент данные является выборкой, содержащей скалярные наблюдения из базового распределения. Элементы данные должны быть совместимы для трансляции в одинаковую форму (за возможным исключением размерности, заданной ось).

статистикаcallable

Статистика, для которой рассчитывается доверительный интервал. статистика должен быть вызываемым объектом, который принимает len(data) образцы как отдельные аргументы и возвращает результирующую статистику. Если векторизованный установлен True, статистика также должен принимать аргумент с ключевым словом ось и быть векторизованными для вычисления статистики вдоль предоставленного ось.

n_resamplesint, по умолчанию: 9999

Количество повторных выборок, выполненных для формирования бутстрап-распределения статистики.

batchint, необязательный

Количество повторных выборок для обработки в каждом векторизованном вызове статистика. Использование памяти составляет O( batch * n ), где n это размер выборки. По умолчанию None, в этом случае batch = n_resamples (или batch = max(n_resamples, n) для method='BCa').

векторизованныйbool, необязательно

Если векторизованный установлен False, статистика не будет передан именованный аргумент ось и ожидается, что она вычисляет статистику только для одномерных выборок. Если True, статистика будет передан аргумент ключевого слова ось и ожидается, что он вычислит статистику вдоль ось при передаче ND-массива выборки. Если None (по умолчанию), векторизованный будет установлено True if axis является параметром статистика. Использование векторизованной статистики обычно сокращает время вычислений.

pairedbool, по умолчанию: False

Обрабатывает ли статистика соответствующие элементы образцов в данные как парные. Если True, bootstrap перевыбирает массив из индексы и использует одинаковые индексы для всех массивов в данные; в противном случае, bootstrap независимо перевыбирает элементы каждого массива.

осьint, по умолчанию: 0

Ось выборок в данные вдоль которой статистика рассчитывается.

confidence_levelfloat, по умолчанию: 0.95

Уровень доверия доверительного интервала.

альтернатива{‘two-sided’, ‘less’, ‘greater’}, по умолчанию: 'two-sided'

Выбрать 'two-sided' (по умолчанию) для двустороннего доверительного интервала, 'less' для одностороннего доверительного интервала с нижней границей на -np.inf, и 'greater' для одностороннего доверительного интервала с верхней границей на np.inf. Другая граница односторонних доверительных интервалов совпадает с границей двустороннего доверительного интервала с confidence_level вдвое дальше от 1.0; например, верхняя граница 95% 'less' доверительный интервал совпадает с верхней границей 90% 'two-sided' доверительный интервал.

метод{‘percentile’, ‘basic’, ‘bca’}, по умолчанию: 'BCa'

Возвращать ли 'процентильный' бутстрап-доверительный интервал ('percentile'), 'basic' (также известный как 'reverse') бутстрапный доверительный интервал ('basic'), или доверительный интервал бутстрапа с коррекцией смещения и ускорением ('BCa').

bootstrap_resultBootstrapResult, опционально

Предоставить объект результата, возвращенный предыдущим вызовом bootstrap включить предыдущее бутстрап-распределение в новое бутстрап-распределение. Это можно использовать, например, для изменения confidence_level, изменить метод, или посмотреть эффект выполнения дополнительной передискретизации без повторения вычислений.

rng{None, int, numpy.random.Generator, опционально

Если rng передается по ключевому слову, типы, отличные от numpy.random.Generator передаются в numpy.random.default_rng для создания экземпляра Generator. Если rng уже является Generator экземпляр, то предоставленный экземпляр используется. Укажите rng для повторяемого поведения функции.

Если этот аргумент передаётся по позиции или random_state передается по ключевому слову, устаревшее поведение для аргумента random_state применяется:

• Если random_state равно None (или numpy.random), numpy.random.RandomState используется синглтон.

• Если random_state является int, новый RandomState используется экземпляр, инициализированный с random_state.

• Если random_state уже является Generator или RandomState экземпляр, тогда этот экземпляр используется.

Изменено в версии 1.15.0: В рамках SPEC-007 переход от использования numpy.random.RandomState to numpy.random.Generator, этот ключевое слово было изменено с random_state to rng. В переходный период оба ключевых слова будут продолжать работать, хотя только одно может быть указано за раз. После переходного периода вызовы функций, использующие random_state ключевое слово будет выдавать предупреждения. Поведение обоих random_state и rng описаны выше, но только rng ключевое слово должно использоваться в новом коде.

Возвращает:

resBootstrapResult

Объект с атрибутами:

confidence_intervalConfidenceInterval

Доверительный интервал бутстрапа как экземпляр collections.namedtuple с атрибутами низкий и высокий.

bootstrap_distributionndarray

Бутстрап-распределение, то есть значение статистика для каждой повторной выборки. Последнее измерение соответствует повторным выборкам (например, res.bootstrap_distribution.shape[-1] == n_resamples).

standard_errorfloat или ndarray

Стандартная ошибка бутстрепа, то есть выборочное стандартное отклонение бутстреп-распределения.

Предупреждает:

DegenerateDataWarning

Генерируется, когда method='BCa' и бутстрап-распределение является вырожденным (например, все элементы идентичны).

Примечания

Элементы доверительного интервала могут быть NaN для method='BCa' если распределение бутстрапа вырождено (например, все элементы идентичны). В этом случае рассмотрите использование другого метод или проверка данные для указаний, что другой анализ может быть более подходящим (например, все наблюдения идентичны).

Ссылки

[1]

B. Efron и R. J. Tibshirani, An Introduction to the Bootstrap, Chapman & Hall/CRC, Boca Raton, FL, USA (1993)

[2]

Натаниэль Э. Хелвиг, «Доверительные интервалы бутстрапа», http://users.stat.umn.edu/~helwig/notes/bootci-Notes.pdf

[3]

Бутстреппинг (статистика), Википедия, https://en.wikipedia.org/wiki/Bootstrapping_%28statistics%29

Примеры

Попробуйте в вашем браузере!

Предположим, у нас есть выборочные данные из неизвестного распределения.

>>> import numpy as np
>>> rng = np.random.default_rng()
>>> from scipy.stats import norm
>>> dist = norm(loc=2, scale=4)  # our "unknown" distribution
>>> data = dist.rvs(size=100, random_state=rng)

Нас интересует стандартное отклонение распределения.

>>> std_true = dist.std()      # the true value of the statistic
>>> print(std_true)
4.0
>>> std_sample = np.std(data)  # the sample statistic
>>> print(std_sample)
3.9460644295563863

Бутстрап используется для аппроксимации изменчивости, которую мы ожидали бы, если бы многократно выбирали выборки из неизвестного распределения и вычисляли статистику выборки каждый раз. Это достигается путем многократного повторного выборки значений из исходной выборки с заменой и вычислением статистики каждого повторного выборки. Это приводит к «бутстрап-распределению» статистики.

>>> import matplotlib.pyplot as plt
>>> from scipy.stats import bootstrap
>>> data = (data,)  # samples must be in a sequence
>>> res = bootstrap(data, np.std, confidence_level=0.9, rng=rng)
>>> fig, ax = plt.subplots()
>>> ax.hist(res.bootstrap_distribution, bins=25)
>>> ax.set_title('Bootstrap Distribution')
>>> ax.set_xlabel('statistic value')
>>> ax.set_ylabel('frequency')
>>> plt.show()

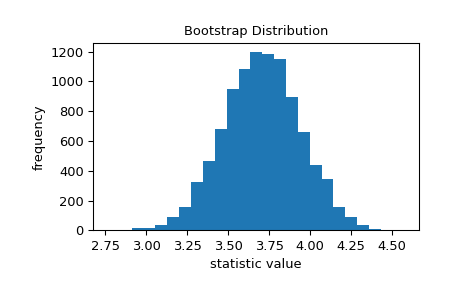
Стандартная ошибка количественно оценивает эту изменчивость. Она рассчитывается как стандартное отклонение бутстреп-распределения.

>>> res.standard_error
0.24427002125829136
>>> res.standard_error == np.std(res.bootstrap_distribution, ddof=1)
True

Бутстрап-распределение статистики часто приблизительно нормально с масштабом, равным стандартной ошибке.

>>> x = np.linspace(3, 5)
>>> pdf = norm.pdf(x, loc=std_sample, scale=res.standard_error)
>>> fig, ax = plt.subplots()
>>> ax.hist(res.bootstrap_distribution, bins=25, density=True)
>>> ax.plot(x, pdf)
>>> ax.set_title('Normal Approximation of the Bootstrap Distribution')
>>> ax.set_xlabel('statistic value')
>>> ax.set_ylabel('pdf')
>>> plt.show()

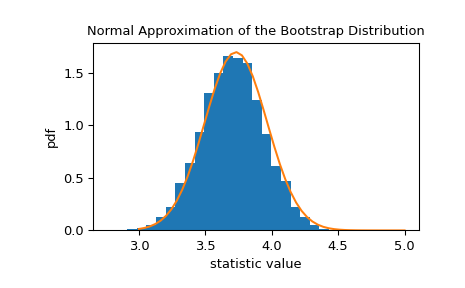
Это предполагает, что мы можем построить 90% доверительный интервал для статистики на основе квантилей этого нормального распределения.

>>> norm.interval(0.9, loc=std_sample, scale=res.standard_error)
(3.5442759991341726, 4.3478528599786)

Благодаря центральной предельной теореме, это нормальное приближение точно для различных статистик и распределений, лежащих в основе выборок; однако приближение не надежно во всех случаях. Потому что bootstrap разработан для работы с произвольными базовыми распределениями и статистиками, он использует более продвинутые техники для генерации точного доверительного интервала.

>>> print(res.confidence_interval)
ConfidenceInterval(low=3.57655333533867, high=4.382043696342881)

Если мы возьмём 100 выборок из исходного распределения и сформируем бутстрап доверительный интервал для каждой выборки, доверительный интервал будет содержать истинное значение статистики примерно в 90% случаев.

>>> n_trials = 100
>>> ci_contains_true_std = 0
>>> for i in range(n_trials):
...    data = (dist.rvs(size=100, random_state=rng),)
...    res = bootstrap(data, np.std, confidence_level=0.9,
...                    n_resamples=999, rng=rng)
...    ci = res.confidence_interval
...    if ci[0] < std_true < ci[1]:
...        ci_contains_true_std += 1
>>> print(ci_contains_true_std)
88

Вместо написания цикла мы также можем определить доверительные интервалы для всех 100 выборок сразу.

>>> data = (dist.rvs(size=(n_trials, 100), random_state=rng),)
>>> res = bootstrap(data, np.std, axis=-1, confidence_level=0.9,
...                 n_resamples=999, rng=rng)
>>> ci_l, ci_u = res.confidence_interval

Здесь, ci_l и ci_u содержат доверительный интервал для каждого из n_trials = 100 выборки.

>>> print(ci_l[:5])
[3.86401283 3.33304394 3.52474647 3.54160981 3.80569252]
>>> print(ci_u[:5])
[4.80217409 4.18143252 4.39734707 4.37549713 4.72843584]

И снова, примерно 90% содержат истинное значение, std_true = 4.

>>> print(np.sum((ci_l < std_true) & (std_true < ci_u)))
93

bootstrap также может использоваться для оценки доверительных интервалов многовыборочных статистик. Например, чтобы получить доверительный интервал для разности средних, мы пишем функцию, которая принимает два аргумента выборки и возвращает только статистику. Использование axis аргумент гарантирует, что все вычисления средних выполняются в одном векторизованном вызове, что быстрее, чем перебор пар повторных выборок в Python.

>>> def my_statistic(sample1, sample2, axis=-1):
...     mean1 = np.mean(sample1, axis=axis)
...     mean2 = np.mean(sample2, axis=axis)
...     return mean1 - mean2

Здесь мы используем метод 'percentile' со стандартным 95% уровнем доверия.

>>> sample1 = norm.rvs(scale=1, size=100, random_state=rng)
>>> sample2 = norm.rvs(scale=2, size=100, random_state=rng)
>>> data = (sample1, sample2)
>>> res = bootstrap(data, my_statistic, method='basic', rng=rng)
>>> print(my_statistic(sample1, sample2))
0.16661030792089523
>>> print(res.confidence_interval)
ConfidenceInterval(low=-0.29087973240818693, high=0.6371338699912273)

Оценка стандартной ошибки методом бутстрэпа также доступна.

>>> print(res.standard_error)
0.238323948262459

Islem BOUZENIA (1) +

>>> from scipy.stats import pearsonr
>>> n = 100
>>> x = np.linspace(0, 10, n)
>>> y = x + rng.uniform(size=n)
>>> print(pearsonr(x, y)[0])  # element 0 is the statistic
0.9954306665125647

Мы оборачиваем pearsonr чтобы он возвращал только статистику, гарантируя что мы используем ось аргумент, потому что он доступен.

>>> def my_statistic(x, y, axis=-1):
...     return pearsonr(x, y, axis=axis)[0]

Мы называем bootstrap используя paired=True.

>>> res = bootstrap((x, y), my_statistic, paired=True, rng=rng)
>>> print(res.confidence_interval)
ConfidenceInterval(low=0.9941504301315878, high=0.996377412215445)

Объект результата может быть передан обратно в bootstrap для выполнения дополнительной передискретизации:

>>> len(res.bootstrap_distribution)
9999
>>> res = bootstrap((x, y), my_statistic, paired=True,
...                 n_resamples=1000, rng=rng,
...                 bootstrap_result=res)
>>> len(res.bootstrap_distribution)
10999

или изменить параметры доверительного интервала:

>>> res2 = bootstrap((x, y), my_statistic, paired=True,
...                  n_resamples=0, rng=rng, bootstrap_result=res,
...                  method='percentile', confidence_level=0.9)
>>> np.testing.assert_equal(res2.bootstrap_distribution,
...                         res.bootstrap_distribution)
>>> res.confidence_interval
ConfidenceInterval(low=0.9941574828235082, high=0.9963781698210212)

без повторного вычисления исходного бутстрап-распределения.

НазадОткрыть во вкладке